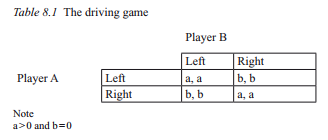
Let us say that we want to explain the emergence of the ‘rules of the road’ and to show how such a convention could emerge merely from the interactions of indi- viduals who do not intend to bring it about. As we want to explain the emergence of the convention, we should start from a situation where no such convention ex- ists. If there are no such conventions, when two people approach each other from opposite directions, they have to make a choice. They may drive on the left, or they may drive on the right. It does not matter which side of the road they choose as far as the other person chooses the same side. This is the only thing that mat- ters, because if they fail to coordinate they may confront hazardous situations. In the terminology of game theory this is a coordination game, as presented in Table 8.1.
In the driving game, ‘Left’ and ‘Right’ are the possible options for players A and B. The letters, a and b, in the table represent the payoffs to their actions. If both player A and player B choose ‘Left’, they have positive payoffs. Similarly, if they both choose ‘Right’ they have positive payoffs. If they fail to coordinate, they do not have positive payoffs. For simplicity, henceforth, we will assume that b = 0. This table tells us that it is in their interest to coordinate. Let us suppose that they have to make their choices simultaneously without any communication. Addition- ally, assume that individuals A and B are rational, that they both know the rules of the game, and that Table 8.1 presents all the information available to them. Given the payoff structure of the game, each player has an incentive to predict what the other will do. The question is, ‘how?’
The driving game is a sample coordination problem2 and, according to Lewis, if a population of agents expects each other to choose a certain action all the time, we may talk about the existence of a driving convention. More properly,
A regularity R in the behaviour of members of a population P when they are agents in a recurrent situation S is a convention if and only if it is true that, and it is common knowledge in P that, in any instance of S among mem- bers of P, (i) everyone conforms to R; (ii) everyone expects everyone else to conform to R; (iii) everyone prefers to conform to R on condition that the others do, since S is a coordination problem and uniform conformity to R is a coordination equilibrium in S.
(Lewis 1969: 58)
That is, if in a society everyone drives on the right; expects everyone else to drive on the right; and prefers to drive on the right on condition that the others do, then we may say that the driving convention in this society is driving on the right-hand side of the road. Briefly, in the driving game, both (right, right) and (left, left) are candidates for becoming a driving convention. Basically, (right, right) and (left, left) are Nash equilibria of this game, or coordination equilibria, in Lewis’s terms.3 An important aspect of this coordination game is that there is no guarantee that the agents will be successful in reaching one of the equilibria (Lewis 1969: 24). In order to explain how conventions emerge, one has to show that coordination is possible and how concordant mutual expectations arise.
Now let us consider the case of two players in order to focus our attention on this point. If two drivers are driving in the middle of the road and have no other information than what is available from the above game-theoretic presentation, they will actually have no way to tell rationally what the other will do. In the terminology of game theory, the two equilibrium points (left-left and right-right), which represent the alternative conventions, are formally indistinguishable and the problem facing the players is known as an equilibrium selection problem. Yet standard game theory suggests that there is also a mixed-strategy equilibrium. In a mixed-strategy equilibrium players randomise their choices according to the payoffs attached to the alternatives. Since the payoffs in this game are symmetric, the mixed-strategy equilibrium of the game consists of the situation where agents choose one of the two alternatives with equal probability (50 per cent, 50 per cent). However, such an equilibrium could not form the basis of a convention. To see this, consider the case for many players: there is no guarantee for success even if all agents mutually expect the others to use a mixed strategy.4 When everybody uses mixed strategies no-one would expect others to conform to a certain pure strategy equilibrium all the time. Agents who continuously use mixed strategies cannot bring about a driving convention.
Moreover, it has been suggested that instead of playing mixed strategies, agents would search for clues for successful coordination. For example, Schelling (1960) argues that existing conventions, norms, personal history, imagination and analogy help individuals to single out one of the many equilibria and help them solve novel coordination problems. Lewis expresses the same idea by arguing that salience and precedence are two important means of creating concordant mutual expectations (see Appendix IV.1 for some examples). In the language of game theory, the equilibrium that stands out among others as a salient option is called a ‘focal-point equilibrium’. Schelling (1960) reported a series of informal experi- ments (see Appendix IV.2) where real individuals were much more successful in coordination than their model counterparts. Lewis and Schelling’s intuition and informal experiments have been confirmed by formal experiments (e.g. Mehta et al. 1992, 1994a,b) that revealed that (‘boundedly rational’) real individuals were much more successful in solving coordination problems than their (hyper)rational model theoretic counterparts. This suggests that real individuals who are con- fronted with the driving game base their expectations about others on the particu- larities of their environment and on history; rather than using mixed strategies.
In general, experiments point out a gap between the ‘predictions’ of standard game theory and the actual behaviour of individuals, a gap that has been con- firmed by a number of other experiments concerning some other games, such as the ultimatum game (e.g. Güth et al. 1982; Henrich et al. 2001, 2005; see Ap- pendix IV.3).5 In sum, it is suggested that in these games real individuals were not doing what the theory predicted them to do and that history, cultural and personal traits, experience and analogies with previous situations are relevant for explain- ing how real individuals behave and how institutions emerge. If this is true then there appears to be an important disparity between the model worlds created by game theorists and the world in which real individuals live.
These experiments support those authors (e.g. Sugden 1998a,b, 2001) who de- mand that explanations of the emergence of institutions should be more empirical. Of course, the idea that ‘institutions and history matter’ is neither new nor surpris- ing. Many institutional economists have demonstrated (e.g. North 1990, Greif 1998) that they do.6 What is surprising may be that many economists and game theorists are convinced that institution-free and history-independent models, such as the driving game, may provide insights about socio-economic phenomena, de- spite the existence of intense criticism and evidence on the contrary. If so many economists are confident that these abstract, ahistorical models have something to contribute, one is tempted to give them the benefit of doubt. It may be that there is some serious misunderstanding between economists who use abstract models and their critics. In order to investigate whether there is such a puzzle, we need to attend to some of the difficulties presented by equilibrium selection and game theory in general.
Source: Aydinonat N. Emrah (2008), The Invisible Hand in Economics: How Economists Explain Unintended Social Consequences, Routledge; 1st edition.
