The last stage of our travel in the world of mixed models brings us to the analysis of models with both moral hazard and nonverifiability. We now assume that the agent first exerts a nonobservable effort that affects the realization of the state of nature, but this state of nature remains nonverifiable, even though its realization is common knowledge between the principal and the agent. The timing of con-tracting is thus exactly the same as in figure 7.6, except that, at date t = 3, the state of nature θ is now observed by both the principal and the agent.
If effort were observable, we would be in the case of models with pure non- verifiability of the state of nature θ. The analysis that we made in chapter 6 shows how the principal and the agent can then agree ex ante, i.e., at date t = 0, on a mechanism, possibly an extensive form game, which ensures that the first-best out- come is uniquely implemented ex post once the state of nature becomes known. How much of this result still holds when effort is not observable by the princi- pal? The answer is quite unsurprising: the first-best can generally no longer be implemented, but the nonverifiability of the state of nature does not bring more distortion than what we find in a model with pure moral hazard and verifiability of the state of nature. In other words, an upper bound of what can be achieved by the principal in a mixed model with moral hazard and nonverifiability is obtained in the model with pure moral hazard, where the state of nature could be described ex ante and used to write the contract. Moreover, this upper bound is actually achieved.
To prove this result, let us consider the pure moral hazard model of sec- tion 4.4. Only the agent’s effort cannot be verified. Assuming that the principal wants to induce a high effort from a risk-averse agent, we know that he must let the latter bear some risk. Still denoting the rents obtained by the agent in each state of nature by 
, the agent’s moral hazard incentive compatibility constraint is written as
The agent’s participation constraint is
Under pure moral hazard, the principal’s problem becomes
Repeating the analysis of section 4.4, we could easily prove that (7.76) and (7.77) are both binding. This yields the following expressions of the moral hazard ex post rents in each state of nature:
and
Moreover, the optimal outputs chosen by the principal in each state of nature are equal to their first-best values: q∗ such that S‘(q∗) = θ when θ realizes, and q¯* such that 
instead realizes. Transfers in each state of nature are thus given by 
.
Figure 7.7 describes these contracts by points AMH and BMH.
We now turn to the case where the state of nature θ is nonverifiable. Let us first consider how ex post negotiations perform in this environment. Assuming that the principal keeps all bargaining power at the ex post bargaining stage, the agent gets zero rent in each state of nature. Anticipating this, the agent has no incentive to exert effort at the ex ante stage. This is an instance of the hold-up problem that we will discuss more extensively in section 9.4.2. Signing an incentive compatible contract with a risk-averse agent at the ex ante stage implies some allocative inef- ficiency, even in the absence of moral hazard, as we know from section 2.11.2. Those inefficiencies can nevertheless be avoided if the agent and the principal agree ex ante to play a mechanism ex post, where both report messages over the state of nature. To implement the pure moral hazard outcome (AMH, BMH), we will thus have to rely on Nash implementation, which now gets all of its strength.
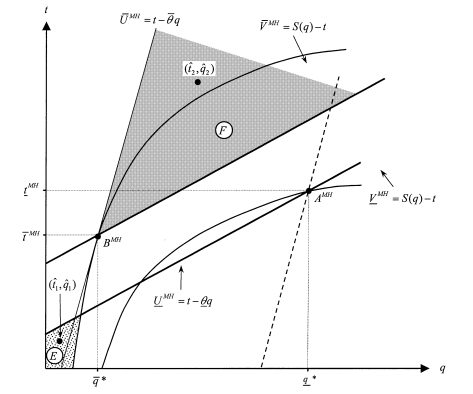
Figure 7.7: Moral Hazard and Nonverifiability
Figure 7.8: Nash Implementation in a Mixed Model
Adopting the same notations as in chapter 6, the game form to be played in each state of nature is illustrated in figure 7.8.
The conditions for Nash implementation of the outcome with pure moral hazard are now easy to obtain.
To have a truthful Nash equilibrium in state θ, we should have
Similarly, to have a truthful Nash equilibrium in state θ¯, we should have
Finally, unique Nash implementation in both states of nature is obtained when
The possible values of 
satisfying the constraints (7.80), (7.83), and (7.85) (resp. (7.81), (7.82), and (7.84)) belong to set E (resp. F ) in figure 7.7.
We leave it to the reader to check that those sets are nonempty and thus the moral hazard contract 
, appended with the out-of- equilibrium punishments 
, allows one to get rid of the nonveri- fiability constraint. Our conclusion is summarized in proposition 7.6.
Proposition 7.6: Mixed models with moral hazard followed by nonverifi- ability of the state of nature do not entail more allocative distortions than those arising in models with pure moral hazard.
The result above relies heavily on the ability of the agents to play a Nash mechanism ex post. Other forms of contracting or not contracting at all will entail significant losses of welfare, contrary to what happened in chapter 6.
Source: Laffont Jean-Jacques, Martimort David (2002), The Theory of Incentives: The Principal-Agent Model, Princeton University Press.