We analyze the questions about the liability of newness in terms of effects on the mortality rate. To begin with the simplest possible model as a baseline of comparison, assume that there is a single overall mortality process driven by a constant rate. In other words, assume that there is a single process by which unions disappear and that it is a Poisson process. The maximum likelihood estimator of the Poisson rate is 0.027. This estimate implies that the expected lifetime of a labor union was 37 years and that the half-life (the age by which half the unions would have experienced mortality) was roughly 26 years.
The claim that organizations face a liability of newness implies that the mortality rate is not constant over age. A nonparametric procedure for exploring whether the mortality rate varies with age is with estimates of the integrated mortality rate (see equation 8.1). Figure 10.1 plots an estimate of this function for the population of labor unions and a 95 percent confidence interval, using Aalen’s (1978) estimator. Recall from Chapter 8 that the integrated rate is approximately a linear function of age if the mortality rate is constant. Clearly the estimated integrated rate is not linear over the age range in Figure 10.1; the integrated rate rises steeply over the first few years of life and then begins to level off. The (pointwise) 95 percent confidence interval is narrow enough that no linear relationships fall within the interval over any considerable age range. So the overall pattern agrees with the argument that organizations have a liability of newness.
In order to describe the process, the integrated mortality rate provides all that we need to know about age variation in the rate for the population taken as a whole. But we want more than description: we want to control for observed characteristics of unions and for unobserved heterogeneity in order to learn whether the age variation apparent in the plot of the integrated rate reflects real aging processes. If there does seem to be a real aging process, we want to explore whether we can summarize the aging process with a simple parametric model. If we can, the task of taking aging into account in studying ecological processes will be greatly simplified.

Figure 10.1 Integrated hazard of mortality of unions (dashed lines indicate 95% confidence interval)
Before turning to the effects of observed and unobserved heterogeneity, we need to discuss the choice of families of parametric models in which to embed the effects of covariates. The recent empirical literature on organi- zational mortality has used the Gompertz model of age dependence and its extension, the Makeham model. As we show next, our research reveals that the Gompertz model does not fit our data as well as the equally simple Weibull model.
In Chapter 8 we pointed out that the Gompertz process implies that the logarithm of the hazard is a linear function of age. So one way to explore the fit of this model is with plots of the logarithm of the estimated values of the hazard against age. This procedure requires that the hazard be evaluated over particular intervals of the time axis. We do so using the classical actuarial estimator of the hazard (Cox and Oakes 1984, pp. 53-56). Figure 10.2 plots the log of the actuarial estimator of the hazard of mortality for national labor unions. If the data were generated by a Gompertz process, this plot would be approximately linear. Rather, the estimated relationship between the log-hazard and age appears to be nonlinear. At young ages, the log-hazards fall above the least squares regression (dashed) line. At middle ages, they fall below the regression line. This poor fit is typical of the results of our explorations with the data described in the previous chapter (Hannan 1988b provides details).

Figure 10.2 Log-hazard of mortality by age for unions
The Weibull model implies a linear relationship between the log-hazard and log-age. Figure 10.3 plots this relationship, again using the actuarial estimator of the hazard. The implied linear relationship seems to hold in Figure 10.3, though it is far from exact. Nonetheless, the fit is better than was the case for the Gompertz model in Figure 10.2. Not only are the observations spread more evenly around the least squares regression line, but the correlation is stronger (—.88 versus —.78). Since the Weibull and Gompertz models have similar qualitative behavior and the Weibull fits these data better, we rely on the Weibull model as the leading alternative to the exponential model as a representation of age dependence in rates of the mortality of labor unions. In so doing, we depart from what has recently become standard practice in organizational demography and ecology.

Figure 10.3 Log-hazard of mortality by log-age for unions
The mortality of labor unions includes three separate processes: merger, absorption, and dissolution. There is no reason to suspect that each subprocess bears the same relationship to age. In fact, the results at every stage in our analysis suggest that the three subprocesses differ substantially. Therefore, we consider them separately in the remainder of this section.
1. The Rate of Disbanding
By disbanding we mean that a labor union dissolved its structure without becoming part of another union. This was clearly the most catastrophic event that could befall a union. The ML estimate of the (constant) rate of disbanding is .011 per year. This rate implies that the expected age of disbanding is 90 and the half-life of unions up to the time of disbanding is about 63 years. But the constant rate understates the importance of this event in the population if there is a liability of newness, since it averages long periods with low rates with the brief periods of very high rates.
Figure 10.4 plots the integrated rate of disbanding against age. Again there is evidence of a strong age dependence: the integrated hazard rises steeply at young ages and then flattens out. This means that the disbanding rate is high at young ages and declines with aging.
Given the results of contrasting the Gompertz and Weibull models dis- cussed above, we begin with the Weibull model of age dependence as an alternative to the exponential (age-independent) model in exploring the effects of covariates. Then we contrast the fit of a model that adds unob- servable heterogeneity in the rate, the gamma model. We also report esti- mates of a generalized gamma model that combines the gamma and Weibull processes. Finally, we examine the results of fitting a model in which the rate can have a non-monotonic relationship with age, the log- logistic model.
As we discussed in Chapter 8, the general model used (from equation 8.12) is
(10.1) log T = -β*x + σW,

Figure 10.4 Integrated rate of union disbanding (dashed lines indicate 95% confidence interval)
where T denotes age at mortality or censoring in this section. The various models we use are special cases of this model. In the case of the exponential (age-independent) model, β* = β, where β is the vector of effects of interest, σ = 1, and W has the extreme value distribution (8.5). In the case of the Weibull model, σ = p-1, β* = βσ, and W again has the extreme value distribution. In the case of the pure gamma model, β* = β, σ = 1, and W has the gamma distribution given in (8.14) with shape parameter k. The generalized gamma model has the same form but without the restriction that σ = 1. Finally, the log-logistic model has β* = β, and W has the logistic density (8.17).
In each stage of the analysis we include six covariates in the models. Two are dummy variables that describe the nature of the starting event. The first (FOUNDING) indicates that the union began with a founding event, as discussed in the previous chapter. The second (SECESSION) tells that the union began when some members left an existing national union and formed a new one. The omitted category includes unions that began with mergers between existing unions and four cases in which professional associations became labor unions. The remaining covariates are four dummy variables that distinguish periods. We use the same set of five periods as in the previous chapter.
Table 10.1 reports ML estimates of the relevant models for disbanding rates of unions. In reporting estimates of these models, we report β rather than – β; that is, we report the negative of the vector of the regression coefficients in equation (10.1). We do so because we are interested in the effects of the covariates on the rates. In the case of the Weibull and generalized gamma models, the negative of the vector of regression coeffi- cients actually estimates β* = βσ, as we pointed out earlier. So the esti- mates reported in the tables can be divided by & to obtain estimates of β.
As we discussed in Chapter 8, σ = p-1 in all models for which this parameter is defined. We report estimates of σ in the tables of findings; these are labeled the “scale parameters.” ML estimates of p equal σ-1 . The tables also report a “shape parameter” for models that use the gamma distribution. The shape parameter equals 1/k2 in the conventions of PROC LIFEREG (SAS Institute 1985).
We begin with an exponential model that holds that the rate does not depend on age once the periods and the covariates are taken into account. In other words, this model holds that there is no structural effect of aging but that the bend in the integrated hazard function reflects only the uncontrolled effects of periods and observed covariates. Estimates of this model can be found in the first column of Table 10.1. The second column reports estimates of a comparable Weibull model, which allows the rate to vary by age. Note that the Weibull model fits significantly better than the exponential model.56 So with this particular model the null hypothesis of age inde- pendence, conditional on the covariates, is rejected decisively.
Table 10.1. ML estimates of models of age dependence in rates of disbanding of labor unions, 1836-1985

Next we consider what happens when we add unobserved heterogene-ity. We begin with a pure gamma model (8.14) which implies that the apparent age dependence reflects the observed covariates and period effects as well as a set of unobserved differences among organizations that have a gamma distribution. The third column in Table 10.1 contains estimates of this model. Although this model represents a significant improvement over the exponential model, it does not fit nearly as well as the Weibull model.
Since both the Weibull and the gamma models improve over the expo- nential model, we are especially interested to learn what happens when we estimate a model that includes both real aging and unobserved heterogeneity. Will the apparent age dependence disappear in such a model? The answer can be found in column 4, which reports estimates of the generalized gamma model. This model does indeed improve the fit significantly compared to the Weibull model.57 So introducing unobserved heterogeneity with a gamma distribution into a Weibull model with these covariates gives a better representation of the process at the cost of a single degree of freedom. However, introducing the unobserved heterogeneity does not eliminate age dependence. A 95 percent confidence interval around the ML estimate of the Weibull scale parameter does not include unity, the value under the null model of an age-independent gamma model. So adding unobserved heterogeneity does not eliminate age dependence—it actually makes it stronger.
The ML estimate of the scale parameter in column 4 of Table 10.1 is 1/2.70 = .37. Figure 10.5 illustrates the average age dependence in the disbanding process implied by this estimate.58 Age dependence in the dis- banding rate has been considerable in substantive terms as well as in terms of statistical significance. For example, the figure shows that the implied rate of disbanding at 2.5 years of age is only half the rate at one year. That is, surviving from age one to age three reduces a union’s disbanding rate by half. Even when observable and unobservable causes of disbandings are taken into account, there is still a substantial liability of newness.
Next we consider the possibility that the rate has a non-monotonic rela- tionship with age. Two previous studies of mortality of labor unions report that mortality rates for unions in the service sector (Langton 1984) and for unions affiliated with the Knights of Labor (Carroll and Huo 1988) declined with age but were lower during the first year than in subsequent years. The possibility that mortality rates are low during the first year makes sense in the case of voluntary associations like labor unions. National unions usually hold annual conventions at which results for the year and prospects for the next year are evaluated. If a union has fared poorly during its initial year, the lack of success becomes particularly apparent at the time of the first convention (the end of the first year). When representatives return to report to the locals, their bad news probably spreads discouragement and speeds the demise of the union.

Figure 10.5 Estimated Weibull disbanding rate
We noted in Chapter 8 that the log-logistic model is a useful one for exploring these questions because it can imply either monotonie or non- monotonic age dependence depending on the value of the shape parameter. In particular, it implies a non-monotonic pattern of age dependence if the scale parameter is less than unity (or equivalently if p > 1 ; see equation 8.16). Since none of the models other than the exponential is a special case of the log-logistic model, we cannot construct a likelihood ratio test of this model against the Weibull or generalized gamma model. Judging from the log-likelihoods, the log-logistic in column 5 fits better than the Weibull and gamma models but not as well as the generalized gamma model. But the important information for our purposes is that the estimate of the scale parameter exceeds unity. Indeed, a 95 percent confidence interval does not include unity. A scale parameter greater than unity implies that the rate of disbanding falls monotonically with age. So this model agrees qualitatively with the others.
One objective of this search among parametric models of age dependence was to find useful representations for incorporating the effects of observed covariates. Of course, this research strategy makes sense only if the covariates actually affect the disbanding rate. Type of starting event makes a huge difference. Unions that started with a founding had disbanding rates that were exp(2.92) = 18.5 times higher than unions that began with a merger. The rate was about eight times larger for unions that seceded than for those that merged. These estimates support Stinchcombe’s arguments about the liability of newness. Existence of prior organization lowers the rate of disbanding. Unions that began by merging two or more existing organizations had the lowest rate of disbanding; those that seceded from an existing organization had the next lowest. And unions that started from scratch as national organizations had the highest disbanding rates.
Although only two of the periods differ significantly from the baseline period running from 1836 to 1886, these differences are also large. Unions that began during the second period, from the start of the American Feder- ation of Labor in 1886 to the start of the New Deal, had disbanding rates about twice as high as those formed during the preceding 50 years. Unions that started during the third period, the New Deal, had disbanding rates that were only a tenth as large as for those formed during the baseline period.
The effect of another covariate, initial size of the union, has special interest. As we mentioned earlier, previous research suggests that the apparent liability of newness may really be a liability of smallness, because new organizations tend to be small and small organizations typically have high mortality rates. If initial size is not considered explicitly, small organi- zations may exit from the population rapidly, driving the average rate in the population down. This is another instance of the general problem that unobserved heterogeneity may give the appearance of negative age depen- dence in transition rates.
Does age dependence persist when we adjust for the size of each union at the time of founding? In order to answer this question, we use data on size of membership in (or near) each union’s initial year, as in the FCH study. Complete information on variations in size after founding is unavailable for many unions. However, given the importance of variations at early ages, use of initial size probably does not seriously limit the scope of our analysis. Even with the use of this more limited measure, cases are lost because initial size is known for only 507 of the 621 unions (this number excludes the 12 unions in the Trade Union Unity League, as noted in Chapter 7).
FCH argued that increasing size affects rates of disbanding at a decreasing rate—that there are diminishing returns to initial scale. They estimated models in which the relationship between size and the rate of disbanding (and merger) was a power function:
![]()
where S0 is initial size and r*( t ) is the rate implied by age dependence and the effects of the covariates. FCH found that initial size had a negative and significant effect on the rate of disbanding and a negative but insignificant effect on the rate of merger.
We use the same specification of the effect of initial size here. We add the logarithm of initial size to the vector of covariates for the generalized gamma model, which has the best fit of the models considered. Since the covariates are constrained to affect the rate log-linearly, this is equivalent to specifying a “power law” relationship between size and the rate of disbanding.
Table 10.2 reports results on the effect of initial size. The first question is whether the subset of cases for which size is known differs systematically from the others. The first column shows that estimating the model in the fourth column of Table 10.1, using only the cases for which initial size is known, produces estimates that are quite similar to those in column 4 of Table 10.1. Although the presence of information on initial size is unlikely to be random, it does not appear that the process of interest differs sub- stantially for the set of unions for which size is known.
The second column in Table 10.2 shows that adding size improves the fit significantly.59 The point estimate of the effect of size, which differs signifi-cantly from zero at the .05 level, is positive—it indicates that initially large unions had higher disbanding rates than smaller ones. This result is the opposite of what FCH found using the subpopulation of large and successful unions.

Because unions that began by merger and secession were much bigger initially on average than those that began with a founding, we explored the possibility that the effects of size differ by type of starting event. The third column in Table 10.2 reports estimates of a model with two effects of size, one for unions that began with a founding and one for unions that began with either a merger or a secession. Using two parameters to represent the effect of size on the disbanding rate does not improve the fit significantly at even the .10 level. Still, the point estimates provide interesting information. The effect of size is positive, strong, and significantly greater than zero for unions that began by merger or secession. The effect is smaller and insignificant, though still positive, for unions that began by founding. These results suggest that initial size did not have much impact on the disbanding rates of newly founded unions but that very big unions created by mergers and secessions faced a strong liability. Perhaps the combination of large membership size and ill-formed organizational routines and structures was especially destabilizing.
From the perspective of this chapter, the most important results in Table 10.2 concern age dependence. Here the pattern is clear: introducing size dependence does not diminish the strength of age dependence. The estimated scale parameters in columns 2 and 3 in Table 10.2 imply that the Weibull parameter is approximately 0.36, which is very close to the level estimated for the entire population without controls for initial size. We conclude that the liability of newness is not an artifact due to omission of initial size (or attributes strongly correlated with initial size) from models for mortality rates.
2. Rates of Absorption
Absorption by another union, with the implied loss of organization, was the second most common ending event for national labor unions. The ML estimate of the constant rate of absorption is 0.08, which implies a half-life to absorption of 86 years. Figure 10.6 plots the integrated rate of absorption by age. Age dependence is again apparent in the nonlinearity of this plot, although the nonlinearity is less pronounced than in the case of disbanding.

Figure 10.6 Integrated rate of absorption of unions by age (dashed lines indicate 95% confidence interval)
Table 10.3 reports estimates of the models for the rate of absorption that parallel those used for rates of disbanding. Again the Weibull model, which allows the absorption rate to vary with age, improves significantly over the exponential model of age independence. The estimated scale parameter for the Weibull model in column 2 implies that the rate decreases slowly with age—the ML estimate of p is 1/1.15 = .87. According to this estimate, the implied age dependence is much less severe than for disbanding.
Unlike the case of disbanding, the pure gamma model of unobserved heterogeneity in the rate of absorption does not improve significantly over the exponential model. Yet the generalized gamma model, which adds unobserved heterogeneity to the Weibull model of age dependence, does fit significantly better than the pure Weibull model. According to the estimates in the fourth column of Table 10.3, the Weibull parameter (p) in this complicated model is 1/1.84 = .54. This means that the rate drops with age even when the effects of unobservables are taken into account. The ML estimate of the gamma shape parameter (.01) implies that there is a large variance in ending times around the distribution implied by the Weibull model.

The substantive case for a non-monotonic pattern of age dependence is stronger in the case of absorption (and the case of equal-status merger, discussed in the following section) than for disbandings. It presumably takes time for these organizational agreements to be worked out and to take effect. Leaders must negotiate agreements, and the membership typically must ratify the agreements before the actual absorption (or merger) takes place. So it would not be surprising if the rate were low initially and then rose with age for a period before beginning its decline with further aging.
Again, we explore the possibility that the absorption rate is low initially, rises with age, and then declines by using the log-logistic model. The fifth column in Table 10.3 reports ML estimates of this model. Note that the log- logistic model fits better than the Weibull model and almost as well as the generalized gamma model (which has one additional parameter). But the estimated scale parameter is very close to unity and its standard error is large, which means that we cannot reject the null hypothesis that the scale parameter equals unity. At the value of unity, the log-logistic model implies monotonic decline from the level implied by the exponential function of the covariates. So there is no suggestion here that the scenario painted above actually characterized the absorption process for unions. We conclude that there was substantial age dependence in the rate of absorption and that this dependence was monotonic-negative. The liability of newness apparently characterized the absorption process as well as the disbanding process.
Effects of several covariates deserve mention. Unions that began with foundings did not differ much, if at all, in absorption rates from those that began with mergers. However, unions that started as secessions were significantly more likely to be absorbed. This makes sense in the context of labor history. Numerous secessions took place over struggles for leadership and over political programs. Seceding groups could sometimes be reincorporated easily into the original union once the disputes had cooled, especially if the protagonists in the original dispute had lost power.
Only one of the periods differs systematically from the baseline: the rate of absorption seems to have dropped sharply during the most recent period. The rate from 1955 to 1985 was only about a fifth as large as during the preceding period.
What happens when we add initial size? Table 10.4 reports our findings. Again the first column reports estimates of the baseline generalized gamma model for the restricted set of cases for which initial size is known. The second column shows the effect of adding size to the model. As was the case for the rate of disbanding, initial size has a strong effect on the rate of absorption. But this time the effect is negative: the rate of absorption for initially large unions was significantly lower than the rate for small ones. Column 3 replaces the single measure of size with separate ones for unions that began with foundings and those that began with some other kind of event. As was the case in our analysis of disbandings, this model does not improve significantly over the model with a single effect of initial size. Nevertheless, the point estimates are again interesting from a substantive perspective. Initial size does not have a significant effect on the absorption rate for unions that began with foundings. However, initial size does have a strong, significant effect for unions that began with mergers or secessions. Most important, adding initial size to the model does not eliminate the apparent age dependence in the rate of absorption. Taking into account the fact that initially larger unions were much less likely to be absorbed, the absorption rate still falls with age.

3. Rate of Equal-Status Merger
The third kind of organizational mortality for labor unions is the merger between two (or more) national unions of roughly equal status that creates a new national union combining the structures into one. The ML estimate of the (constant) rate of merger is 0.08, essentially the same as the rate of absorption. Figure 10.7 reports the estimated integrated rate of equal- status merger by age. Again a pattern of age dependence is apparent in the nonlinearity of this plot. The rate during the early years seems higher than in later years. The pattern resembles that for absorption and is again weaker than for disbanding.
Table 10.5 reports ML estimates of models of the rate of equal-status merger. Since the pattern of effects is fairly similar to those just discussed for absorption, we do not discuss them in detail.60 According to the Weibull model, the rate of equal-status merger declines with age.
While the pure gamma model fits about as well as the Weibull model, we never succeeded in obtaining estimates of the generalized gamma model for this outcome. So we do not have any formal way to examine whether the merger process reflects both a liability of newness of the Weibull form and unobservable heterogeneity.
As was the case for the other two rates, the estimated log-logistic model implies that the rate of equal-status merger declines monotonically with age, because the estimated scale parameter exceeds unity. Therefore, as in the case of the other two rates, we conclude that labor unions have faced a liability of newness with respect to the merger process and that this liability falls monotonically with age.
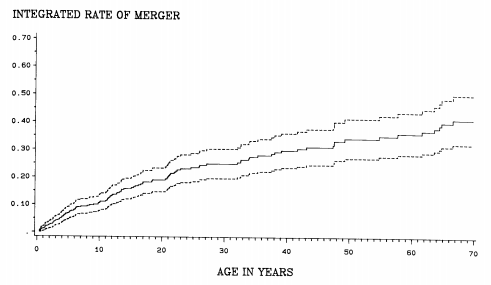
Figure 10.7 Integrated rate of equal-status merger by age (dashed lines indicate 95% confidence interval)
4. Comparisons with Previous Findings
This replication of the FCH analysis of age dependence in the mortality of national labor unions finds one major consistency with the earlier work and one major difference. The consistency concerns the main question. The research reported here agrees with FCH that Stinchcombe (1965) was right the demography of national labor unions has been characterized by a strong liability of newness. This liability of newness applies to the overall process of mortality and to each of the three component processes: disbanding, absorption, and merger.
The divergence from FCH concerns the effects of size on mortality. Although both studies found that the liability of newness was not primarily a liability of smallness, the findings about the effects of size differ consider- ably. FCH found that larger unions had smaller rates of disbanding; the present research finds the opposite pattern. FCH found no significant effect of size on the merger rate; the present study, which uses more complete data, finds that size has strong and significant effects on one component of the overall merger rate, the rate of absorption into other unions. Larger unions had significantly lower rates of absorption than smaller ones. However, this research finds no strong evidence that size affected the rate of equal-status merger.

Interestingly, initial size did not affect any of the rates for unions that began with a founding, according to our estimates. The significant positive effect of size on the disbanding rate and the significant negative effect of size on the absorption rate seem to have held mainly for unions that began with a merger or a secession. Perhaps large unions starting through such processes tend to be weak. Since large unions can only be absorbed by other large unions, a big union in trouble is more likely to disappear through disbanding than through merger.
The set of parametric models used here also differs from those used by FCH. While FCH used Gompertz and Makeham models, this research finds that Gompertz models fit data on union lifetimes less well than comparable Weibull models. This research also estimated models that combined unobserved heterogeneity, a generic cause of “spurious age dependence’’ with aging. Even though adding unobserved heterogeneity (assumed to follow a gamma distribution) typically improves the fit of a Weibull model significantly, it does not eliminate the significant age dependence in these mortality processes. So we have some evidence that the liability of newness concerns real effects of aging rather than simply the early loss of unions with (unobserved) low levels of fitness.
Finally, we explored the reasonable supposition that organizational mor- tality rates increase with age initially before beginning to decline with aging. We did so using the log-logistic model. Although this model often fit the data as well as the others, estimates of its parameters suggest that the age dependence in these rates was monotonic.
Source: Hannan Michael T., Freeman John (1993), Organizational Ecology, Harvard University Press; Reprint edition.
