Next we consider the lengths of “careers’’ in the semiconductor industry, the length of time between entry and exit of firms. Limitations on the data preclude an analysis with as much detail as just reported for labor unions. Entries and exits are recorded only at yearly intervals in the data we used; so observed durations in the industry are also aggregated in time. Since more than half the firms in the population had observed durations of three or fewer years in the semiconductor industry, the temporal aggregation is large relative to the time scale of events.61
Given the temporal aggregation of these data, we display the qualitative pattern of variation in exit rates with length of time in the industry using the actuarial estimator of the hazard. Figure 10.8 plots the estimated haz-ard by years in the industry over the observed range. This plot suggests a pronounced liability of newness. The hazard during the first year in the industry is considerably larger than for any other year. From this initial high level, the hazard of exit drops fairly consistently with number of years in the industry, falling to zero toward the upper end of the observed range. In other words, the rate of exit drops roughly monotoni- cally with time in the industry. There does seem to have been a liability of newness.
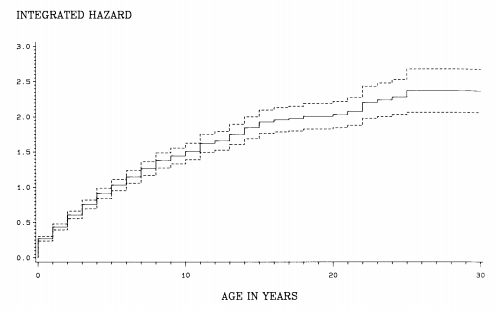
Figure 10.8 Integrated hazard: semiconductor firm mortality (dashed lines indicate 95% confidence interval)
In the spirit of the previous section, we next explore whether the pattern of decline in the rate agrees with a Gompertz or a Weibull model. Recall that the Gompertz model implies that the log-hazard is a linear function of elapsed time and the Weibull implies that it is a linear function of the logarithm of elapsed time. Figures 10.9 and 10.10 display these two plots. Both plots seem to fit reasonably well. The correlation is slightly higher for the relation of the log-hazard to log-time (-.84 versus -.82), but this difference is too small to form the basis of a choice of specifications. However, the linear relationship between the log-hazard and elapsed time, which follows from the Gompertz model, does not fit well in the lower range of the time scale. Note in Figure 10.9 that the first five observations (in time) fall above the regression line whereas the same observations fall around the regression line in Figure 10.10. This difference suggests that the Gompertz model understates the hazard at short durations, the period of most interest from the perspective of arguments about a liability of newness. Therefore we use an approximation of the Weibull model (and the generalized gamma model) in analyses in subsequent chapters that introduce the effects of changing covariates.

Figure 10.9 Log-hazard of semiconductor firm exiting by duration

Figure 10.10 Log-hazard of semiconductor firm exiting by log-duration
We also wanted to learn how conditions at time of founding and unob- served heterogeneity combined with aging in affecting exit rates. We have done this in two ways. In one, we assigned to each firm the midyear of its final year as the date of exiting. In the other, we assigned each firm an exiting date that is the sum of the difference between its exiting year and entering year and a random number uniformly distributed between zero and one. We then applied the variety of models discussed earlier in the chapter to these two sets of observations. The two analyses agree that the generalized gamma model fits significantly better than any of its special cases. In particular, the results tell that there was substantial unobserved variation in exit rates and a strong liability of newness.
The analyses reported in this chapter point in a fairly clear direction. We find that failure rates are monotonic functions of age (or duration in the industry, in the case of semiconductor firms). We also find that the simple Weibull model appears to provide a better representation of this process than the Gompertz model, which has formed the basis of most previous research on this subject. Finally, we find that adding unobserved heterogeneity sometimes improves the fit of Weibull models significantly but does not alter conclusions about the presence of age dependence in the rates. We build on these results in the remaining chapters. In particular, we begin with Weibull models in analyses of density dependence and niche width, and we explore the consequences of adding unobserved heterogeneity to these models. We begin in the next chapter with the effects of density on failure rates.
Source: Hannan Michael T., Freeman John (1993), Organizational Ecology, Harvard University Press; Reprint edition.
