True equilibria in closed systems and stationary “equilibria” in open systems show a certain similarity, inasmuch as the system, taken as a whole and in view of its components, remains constant in both systems. But the physical situation in both cases is fundamentally different. Chemical equilibria in closed systems are based on reversible reactions; they are a consequence of the second principle of thermodynamics and are defined by minimum free energy. In open systems, in contrast, the steady state is not reversible as a whole nor in many individual reactions. Furthermore, the second principle applies, by definition, to closed systems only and does not define the steady state.
A closed system must, according to the second principle, eventually attain a time-independent state of equilibrium, defined by maximum entropy and minimum free energy (heat equilibrium, thermodynamic derivation of the law of mass action by van’t Hoff, etc.), where the ratio between the phases remains constant. An open chemical system may attain (certain conditions presupposed) a time-independent steady state, where the system remains constant as a whole and in its (macroscopic) phases, though there is a continuous flow of component materials.
A closed system in equilibrium does not need energy for its preservation, nor can energy be obtained from it. For example, a closed reservoir contains a large amount of (potential) energy; but it cannot drive a motor. The same is true of a chemical system in equilibrium. It is not a state of chemical rest; rather reactions are continually going on, so regulated by the law of mass action that as much is formed of every species of molecules or ions as disappears. Nevertheless, the chemical equilibrium is incapable of performing work. For maintaining the processes going on, no work is required nor can work be won from it. The algebraic sum of work obtained from and used by the elementary reactions equals zero. In order to perform work, it is necessary that the system be not in a state of equilibrium but tend to attain it; only then can energy be won. In order that this is achieved continually, the hydrodynamic as well as chemical system must be arranged as stationary—i.e., a steady flow of water or chemical substances must be maintained whose energy content is transformed into work. Continuous working capacity is, therefore, not possible in a closed system which tends to attain equilibrium as soon as possible, but only in an open system. The apparent “equilibrium” found in an organism is not a true equilibrium incapable of performing work; rather it is a dynamic pseudo-equilibrium, kept constant at a certain distance from true equilibrium; so being capable of performing work but, on the other hand, requiring continuous import of energy for maintaining the distance from true equilibrium.
For the maintenance of “dynamic equilibrium,” it is necessary that the rates of processes be exactly harmonized. Only in this way is it possible that certain components can be broken down, so liberating usable energy while, on the other hand, import prevents the system from attaining equilibrium. Fast reactions, also in the organism, lead to chemical equilibrium (e.g. of hemoglobin and oxygen); slow reactions do not reach equilibrium but are kept in a steady state. Therefore, the condition for the existence of a chemical system in a steady state is a certain slowness of reactions. Momentary reactions, like those between ions, lead to equilibrium in “infinitely short” time. The maintenance of a steady state in the organism is due to the fact that it is composed of complex carbon compounds; these are, on the one hand, rich in energy but chemically inert, so that the maintenance of considerable chemical potential is possible; on the other hand, rapid and regulated release of this amount of energy is performed by enzyme actions, so that a steady state is maintained.
For deriving conditions and characteristics of steady states we may use a general transport equation. Let Qi be a measure of the i-th element of the system, e.g. a concentration or energy in a system of simultaneous equations. Its variation may be expressed by:
Ti represents the velocity of transport of the element Qi in a volume element at a certain point of space, while Pi is the rate of production.
Many equations appearing in physics, biology and even sociology, can be considered as special cases of (5.1). For example, in molecular magnitude, the Pi are functions indicating the rate of reactions by which the substances are formed and destroyed; the Ti will have different forms depending on the system concerned. If, for example, no outer forces influence the masses, the Ti will be expressed by Fick’s diffusion equation. In case Ti disappears, we have the usual equations for a set of reactions in a closed system; if Pi disappears, we have the simple diffusion equation where Ti has the form: 
, the Laplacian symbol ∇2 representing the sum of the partial derivatives in x, y, z, the Di the diffusion coefficients. In biology, equations of this type are found, e.g., in growth; and they appear in sociology and . population dynamics. In general, the rate of change of a population equals the population movement (immigration minus emigration) plus rate of reproduction (birth minus death rate).
In general, we therefore have a set of simultaneous partial differential equations. Pi as well as Ti will, in general, be nonlinear functions of and other system variables and furthermore functions of the space coordinates x, y, z and time t. For solving the equation, we must know the special form of the equations, and the initial and limiting conditions.
For our purpose, two considerations are important, which we may call temporal cross and longitudinal sections. The first problem is the maintenance in a steady state which, biologically, is the fundamental problem of metabolism. The second concerns changes of the system with respect to time, biologically expressed, e.g. as growth. Briefly we shall also mention a third problem— i.e., periodic changes as, in the organismic realm, are characteristic of autonomic processes such as automatic-rhythmical movements, etc. These three aspects correspond to the general problems of the three main fields of physiology (cf. pp. 12If.).
The problem of “longitudinal temporal section,” of the changes of the system in time, will be answered by solution of differential equation of type (5.1).
As a simple example, consider an open chemical system, consisting of only one component Q, reaction material being continually imported and resulting reaction products removed. Let E be the amount of imported reaction material per time unit; k, the reaction constant according to the law of mass action; kQ, therefore, the amount of change per time unit; then, presupposed the amount imported at the beginning is greater than that transformed, the concentration of the system will increase according to the equation:
As is easily seen, this is a special case of the general equation (5.1). Since inflow was assumed to be constant and outflow equal to the chemical reaction, hence diffusion and concentration gradients were neglected (or, as may be said, a complete “shaking” of the system was assumed), the space co-ordinates in (5.1) disappear; instead of a partial, we have an ordinary differential equation. Concentration at time t then is:
Qq being the initial concentration at t = 0. Concentration therefore asymptotically increases to a certain limit where turnover equals inflow (assumed to be constant). This maximal concentration is Q∞ = E/k.
A system more approaching biological conditions is as follows. Let there be transport of material a1 into the system proportional to the difference between its concentration outside and inside of the system (X—x1). Biologically, we may here think of simple sugars or amino acids. The imported material a1 may form, in a monomolecular and reversible reaction, a compound a2 of concentration x2 (e.g. monosaccharids transformed into polysaccharids, amino acids into proteins). On the other hand, the substance a1 may be catabolized in an irreversible reaction (e.g. oxidation, desamination) into a3; and a3 may be removed from the system, proportional to its concentration. Then we have the following system of reactions:
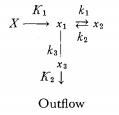
and equations:
For eliminating the constant in the first equation, equate it to 0; x1*, x2* … be the roots of these equations. We introduce as new variables:
and reformulate (5.4) accordingly.
The general type of such equations is:
with the general solution (cf. p. 58):
The X’s are given by the characteristic equation:
We now consider the temporal cross-section, i.e. the distribution of components in the time-independent steady state.
In general, a system defined by equation (5.1) can have three different solutions. First, there can be unlimited increase of the Qi, secondly, a time-independent steady state may be attained; thirdly, there may be periodic solutions.
It is difficult to prove the existence of a steady state for the general system (5.1), yet it can be shown in certain cases. Suppose that both terms are linear in the £X and independent of t. Then the solution can be found by standard methods of integration and is of the form:
where Qi2 is a function of t which with increasing time is decreas ing to zero for certain relations between constants and limiting conditions.
If, on the other hand, there is a time-independent steady state expressed by Qi1, in (5.9), Qi1 must suffice for
From this we see:
- If there is a stationary solution, the composition of the system in the steady state remains constant with respect to the components Qi although the reactions continue and do not reach equilibrium as in a closed system, and although there is inflow and outflow of material; the situation so highly characteristic of organismic systems.
- In the steady state the number of elements entering state Qi (x, y, z, t) by transport and chemical reaction per time unit equals the number leaving it.
Similar considerations can be made with respect to periodic solutions. It is true that the above derivation presupposes rather special assumptions on the nature of the equations. However, although no general criterion is known for the existence of stationary and periodic solutions in system (5.1), these conditions can be indicated for certain types of linear and even non-linear cases. Important to us is the fact that the existence of stationary, dynamic “equilibria” in open systems, or as we may also say, the existence of a certain order of processes guaranteed by dynamic rather than structural-mechanical principles, can be derived from general considerations.
Solving equations (5.4) for the steady state we obtain:
We therefore see that in the steady state a constant ratio between the components is established although it is not, as in a closed system, based on an equilibrium of reversible reactions, but the reactions are partly irreversible. Moreover, the ratio of components in the steady state depends only on the reaction constants, not on the amount of the inflow; the system thus shows “self-regulation,” comparable to organismic systems, where the ratio of the components is maintained in changing inflow, changing absolute size, etc.
Furthermore we find:
In case an external disturbance (“stimulus”) leads to increased catabolism—e.g., increase of the reaction constant k3 while the other constants remain unaltered—decreases. Since, however, inflow is proportional to the concentration difference X—»q, with increase of the latter intake is increased. If, after cessation of the “stimulus,” the constant of catabolism returns to its normal value, the system will return to its original state. If, however, the disturbance and hence the change of rate of catabolism persists, a new steady state will be established. Thus the system develops forces directed against the disturbance, tending to compensate increased catabolism by increased intake. It therefore shows “adaptation” to the new situation. These, too, are “self-regulative” characteristics of the system.
It can, therefore, be seen that the properties indicated as characteristic of organismic systems, are consequences of the nature of open systems: maintenance in “dynamic equilibrium,” independence of composition of the absolute quantity of components, maintenance of the composition under changing conditions and nutrition, reestablishment of dynamic equilibrium after normal catabolism or catabolism increased by a stimulus, dynamic order of processes, etc. “Self-regulation of metabolism” can be made understandable on the basis of physical principles.
Source: Bertalanffy Ludwig Von (1969), General System Theory: Foundations, Development, Applications, George Braziller Inc.; Revised edition.