Models have many uses in everyday life, in science and in philosophy of science. Models might be material, visual, formal or representational, theoretical, or im- aginary. Mäki (2001a) argues that there is one thing common to all these different types of models: ‘they represent something beyond themselves’.13 In this sense, we may consider the chequerboard model of residential segregation as a repre- sentation of the way in which segregation emerges in the real world. But what is the nature of this representation? To see this let us start by examining how we can represent an already known particular phenomenon, and gradually introduce the types of issues that are relevant in modelling social phenomena.
1. Isomorphisms
Basically, any ‘environment can in principle be described by a set of states and a transition function (or next state function) that specifies how the states change overtime’ (Holland et al., 1989: 30).14 Thus, a model characterising an environ- ment like a city with a focus on segregation patterns may describe the city to be in a state where there is no segregation, and in another state where there is segregation. A transition function, then, can be characterised with the elements in the model that carry the city from the first state to the other. Thus, the transition function(s) (of the model, T’ in Figure 7.1) represents the causal mechanisms that bring about segregation.
Assume now, for the sake of the argument, that we have all sorts of informa- tion about a particular city (City A) concerning its states prior to and after the emergence of segregation. We also have a considerable amount of information about individuals’ motivations and discriminatory preferences and about the way in which two different ethnic groups are distributed in City A. Yet we do not know why and how segregation emerged. That is, we have all sorts of information about R-World (t) and R-World (t + n), but we do not know the way in which R-World (t) was transformed into R-World (t + n). We want to know the mechanisms (T) that have contributed to the emergence of segregation.

Figure 7.1 Model world and the real world (adapted from Holland et al. 1989).15
What would a model of this transition look like? We may start with a detailed description of R-World (t) and R-World (t + n) (i.e. describing every individual, neighbourhood, action, etc.). We may also try to present a detailed picture of every state of City A from no-segregation to segregation.16 But a description where every aspect of the city finds a place would be like the city itself and would be too complex to tell us something about the way in which segregation emerged in this city. That is, it would be hard to build a model that is isomorphic to the city it represents (i.e. where there is a one-to-one relation between the model city and the real city). Simply, a complete description of what we know about the city is not very informative, or it is too complex to tell us something.17
2. Abstractions and q-morphisms
One important concern about how to represent the transition of a real city from one state to the other is that the real world is usually too complex to be modelled in this way. Thus, it is ‘unreasonable to expect’ models ‘to be isomorphisms in which each unique state of the world maps onto a unique state in the model’ (Hol- land et al. 1989: 31). A fundamental component of thinking about the world is abstraction. Holyoak and Thagard (1996: 19–20) remind us of a story of Jorge Luis Borges, Funes the Memorious, in which the fictional character Ireneo Funes has an exceptionally good memory to remember every detail in his life. But his alertness to details makes him incapable of abstract reasoning.
Not only it was difficult for him to comprehend that the generic symbol ‘dog’ embraces so many unlike individuals of diverse size and form; it bothered him that the dog at three fourteen (seen from side) should have the same name as the dog at three fifteen (seen from the front).
Borges’s story suggests that abstraction is extremely useful for our reasoning and it guides our inferences, which usually go beyond our direct observations and mere descriptions of the real world.
Neither ordinary human beings nor scientists can reason without abstraction. The model builder is then forced to form general concepts and to simplify the model by ignoring unnecessary or irrelevant components of the world for the specific task at hand. In daily life we use such categorisations and abstractions quite naturally without much thinking, yet to build a model we also need con- scious thinking about the way in which certain entities should be characterised, categorised, etc. For example, for the case of segregation, we may categorise individuals into different categories, such as racist individuals, individuals who prefer a mixed neighbourhood, individuals who cannot tolerate a certain minority status, etc. Or, we may categorise individuals into different groups, such as indi- viduals who have above-average income, average income, low income, etc. Note also that ‘segregation’ itself is an abstraction and that such categorisations are not independent from our existent state of knowledge.
Having formed certain categories and generalisations, we may use them in our model. But this time the relation between our model city and the real city is not isomorphic (in the sense defined above). Rather it is a many-to-one – that is, homomorphic – relation. ‘A faithful model based on categories, in which the mapping from elements of the world to elements of the [model] is many-to-one, is called homomorphisms’ (Holland et al. 1989: 31). Indeed, this is what happens in many economic models: certain concepts in our models, such as the consumer and the producer, represent many individuals.
However, it is also true that our categorisations and generalisations are not exceptionless. For example, if we represent several individuals who prefer a mixed neighbourhood with a few model agents, and homogenise their prefer- ences concerning their neighbourhoods, we may overlook the fact that some of the (real) individuals may be more tolerant to a minority status than others. Our representation of the states of City A would most probably be incomplete, subject to exceptions. Generally, our models of the world are typically far from perfect, that is, the mapping between the model world and the real world is flawed. In Holland et al.’s terminology, such mappings are called quasi-homomorphisms (q- morphisims). Considering the case of segregation, this means that our model of the transformation of R-World (t) to R-World (t + n) is likely to be incomplete, and the relation between R-World and M-World would be q-morphic.
3. Isolation
The fact that our models of the real world are usually q-morphic implies that they are deformed images of the real world. Yet such deformations are necessary for dealing with the complex real world, that is, for understanding, for living in, etc.
Faced with the essential complexity of the world, every science is compelled to employ methods of modifying and deforming it so as to make it or the image of it theoretically manageable and comprehensible.
(Mäki 1992a: 317)
We have seen that one of the tools that helps us represent the real world in a comprehensible manner is abstraction and that it is a subspecies of isolation (see Chapter 4, note 10). We use the method of isolation in everyday life, consciously or unconsciously. We use abstractions and we also idealise the environment we are living in. Likewise, scientists isolate; they focus on some factors rather than the others, given their initial hypothesis about the way in which a certain fact may be explained. As Mäki would agree, one-to-one representations of the real world phenomena are intractable. This is one reason to utilise the method of isola- tion. But more importantly, the ability to isolate is the key to understanding the world.20
4. Analogical thinking
But how do we choose the factors that are relevant, that is, those to be isolated from the influence of others? Until now we have implicitly assumed that it is pos-sible to model the transformation of City A from a state with no segregation to a state with segregation. Yet the real problem in modelling this transformation is to discover a way to represent it, a way that would tell us something about the real world. If we do not have any idea about the way in which segregation may have emerged, it would be practically impossible to present a model of the emergence of segregation. Having an initial hypothesis about the way in which segregation may have emerged is certainly necessary for building a model of this process. Generally, scientists do not start their investigation from scratch. They have cer- tain ideas about what may have caused a certain phenomenon, or what may be relevant in explaining a certain fact. Obviously, not all the available information about the states of City A would be relevant in explaining the emergence of seg- regation in this particular city. For example, we may ignore the data about the shoe sizes of the individuals, or the type of armchairs they use as being irrelevant to, or having negligible impact on, the emergence of segregation. Selecting the seemingly relevant factors is not independent from our existing state of knowl- edge about the world, about the things we know about segregation in general, and about other aspects of social life. What we know about the real world helps us conjecture about the factors that may be relevant, and to formulate an initial hypothesis about the way in which segregation may have emerged. When we try to build models, we usually go beyond simple statements of bits of information, or mere descriptions of what we observe, and our model depends on, or starts from, our initial (i.e. prior to model building) knowledge about the world. For this reason, model building certainly involves some type of analogical or metaphori- cal thinking.
One fundamental purpose of analogy is ‘to gain understanding that goes be- yond the information we receive from our senses’ (Holyoak and Thagard 1996: 9). Human beings recognise similarities between what they observe and what they already know about other things, and usually if they find enough (or some) similarities between two different phenomena, they use these similarities to rea- son about the relatively less-known phenomenon. If we are allowed to use ‘anal- ogy’ in a loose way, we may say that all we know about our neighbours, how they react to or interact with another ethnic group, or the things we know about social behaviour, individuals’ reactions to social differences, etc. may help us in form- ing an idea about the way in which segregation may have emerged in City A. Of course, analogical or metaphorical thinking cannot be the definite source of our knowledge. But it may help us form our initial hypothesis about the emergence of segregation. That is, ‘analogy is a source of plausible conjectures, not guaranteed conclusions’ (Holyoak and Thagard 1996: 30).
Simple analogical thinking involves the discovery of the similarities and dif- ferences between objects, and of relations in two different domains. Most of our everyday explanations make use of similarities between causal relationships in two different domains. Moreover, scientific explanations involve more complex high-order relational and causal mappings, as well as the use of metaphors.21 The ability to map what we observe onto what we already know is an important mecha- nism that makes us generate thoughts about what we are trying to explain. We find out what we believe to be the relevant relationships about a phenomenon by con-ceptualising it in light of our existing knowledge together with our observations about the phenomenon to be explained. In short, what we know about the real world helps us generate fallible hypotheses or conjectures about the way in which a certain phenomenon may be explained.22
5. Representation
Now, let us assume that what we know about segregation is the following: we know that there are people who have strong discriminatory preferences, and that there are welfare differences between two ethnic groups. We also know that ex- isting accounts of the emergence of segregation suggest that these two factors explain segregation in other cities. Then, other models of residential segregation may help us single out the relevant factors for our own model, and study their relation in isolation from other factors. That is, we may infer that what is true for other segregated cities may also be true for City A, and start our modelling from here. This helps us categorise and organise the available information and try to see whether such and such is really the case for City A.
Briefly, given what we know about segregation, we may isolate a couple of factors, strong discriminatory preferences and welfare differences, and try to see whether emergence of segregation in City A can be explained by these factors. In this case, our task is to show how these factors interact in bringing about segrega- tion in City A. The only thing we have to do is to check whether our initial hy- pothesis is confirmed by what is known about City A. If this is the case, we would have a singular explanation of the emergence of segregation in City A. Yet the reader may object that we hardly have a theoretical model of segregation in this case, rather, what we did is to use the existing models / theories of segregation to explain another instance of segregation. This is true. We have explained segrega- tion in City A with the help of previous ‘theories’ of the emergence of segregation. Models of this type do not provide new insights about general phenomena; rather, they confirm previous insights and generalisations, and help us explain new par- ticular cases. As we have seen in the previous chapters, this is not what happens in explaining unintended social consequences.
Until now, we have assumed that modelling starts from particulars and models represent particulars. Remember that ‘in an isolation, something, a set X of enti- ties, is “sealed off” from the involvement or influence of everything else, a set Y of entities; together X and Y comprise the universe’. The elements of the set of X entities need not be particulars. Yet we have seen that ‘explanation as re- description’ is sometimes wrongly interpreted as suggesting that models represent particular phenomena.23 The practice of modelling does not always start from par- ticulars, rather scientists try to model a general phenomenon (e.g. the emergence of segregation in general) and consider a set of other generalisations and concepts in isolation from others to be able to model segregation. To see this, consider the case of the emergence of segregation again.
Figure 7.2 pictures a possible way in which we may conceptualise segregation prior to our modelling efforts. What we know is that there are many residentially segregated cities, and that segregation in general is explained with strong dis- criminatory preferences, organised action and welfare differences. That is, our initial conception of segregation can be considered as a general (mental) model about segregation. We start our examination of residential segregation from this general conception of segregation, that is, given what we know about segrega- tion. This means that what we have characterised as the real world (what has been characterised as R-World before) may be considered as a ‘model’ itself; it is our conception of the real world, which is characterised by many generalisations and isolations. We rarely build theoretical models of particular phenomena from scratch; we usually have a mental image of them and start from there. Scientists build theoretical and empirical models to refine this image.
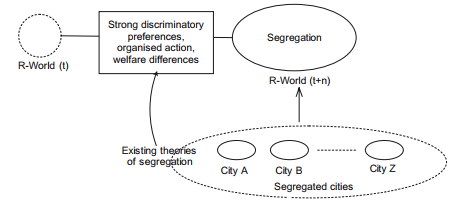
Figure 7.2 A possible way to conceptualise segregation.
Let us assume now that our knowledge of residential segregation has other aspects; particularly that we also know that there have been many attempts to reduce the degree of segregation in different cities. Known policy interventions against segregation focused on reducing welfare differences among different eth- nic groups, and banned and controlled possible types of organised action that may prevent the formation of integrated neighbourhoods (e.g. public policies for moni- toring housing agencies). Yet these policies were unsuccessful in reducing the amount of residential segregation, and residential segregation persisted despite these acts and controls.24 Given this knowledge, we may suspect that there may be other causes of segregation; that is, other than strong discriminatory prefer- ences, organised action and welfare differences. In particular, we may suspect that individuals may be segregated because many individuals enjoy living with similar others, and living as an extreme minority is not something that everyone would prefer. Of course such an intuition does not come from nowhere. Our ex- isting knowledge of social sciences helps us in forming this initial hypothesis. For example, we may know that there are unintended social consequences, and that social psychology suggests that individuals do not like living in an extreme minority status.25 The question is whether there is another mechanism of segrega-tion rooted at the individual level that may produce segregation as an unintended consequence of human action. The problem is that we do not know any city where these other factors were absent and we know very little about the actual prefer- ences of individuals. In general, we do not know enough about R-World (t) to show that segregation may indeed emerge as an unintended consequence of hu- man action.
What we need to do is study the conditions under which segregation may emerge, and in order to be able to focus on the effects of mild discriminatory preferences we may isolate them (in our model) from other known causes of segregation (e.g. from organised action). Note that when we look at aggregate statistics about segregated cities, we cannot deduce the type of preferences indi- viduals have. Even if we have some data about the preferences of individuals, we know that individuals are diverse and their preferences range from being highly tolerant about other ethnic groups to zero-tolerance. This may make our task very complex. On the other hand, if we start our analysis from a particular city, where segregation is somewhat simultaneous with the arrival of a new ethnic group, it may be difficult to understand the extent to which mild discriminatory prefer- ences may be responsible for segregation. Thus, it may be a good idea to build a model where we can study the emergence of segregation in isolation from the complexities of the real world. Now consider Schelling’s effort to show that mild discriminatory preferences may be responsible for segregation. His preference was to ‘postulate some mechanisms and see whether they produce segregation’. The chequerboard city is a model that represents cities that have at least two dif- ferent ethnic groups. But it is not in any way a representation of the emergence of segregation in any particular city. Rather, it is constructed to test the initial hypothesis that segregation may be an unintended consequence of human action. It is constructed, yet it is based on knowledge of how things work (or may work) in the real world.
To build the chequerboard model we start from the picture presented in Fig- ure 7.2 and we conjecture about the ways in which segregation may emerge in the absence of organised action and welfare differences (see Figure 7.3). It is true that the chequerboard model represents the emergence of segregation and that the chequerboard city represents real cities, but in a special way. Not all the characteristics of the chequerboard model and what happens therein have been previously observed. The model is rather constructed with some modification and rearrangement of what we know about segregation and, most importantly, it is constructed to present a what-if scenario. Several types of isolation, as well as some conjectural construction, are at work here. The view that considers models merely as representations or explanations as re-descriptions fails to convey this idea, and for this reason it is open to misunderstanding.
Representations need not start from concrete phenomena and in economics they usually do not. Economists and other social scientists usually start model- ling from our everyday conceptualisations of phenomena (see Mäki 1996: 434). Yet what makes economics different from folk views concerning economic phenomena is that economists ‘rearrange’ and ‘modify’ these everyday (mental) representations to gain a better understanding of the general facts to be explained (Mäki 1996).26 Models in this sense are webs of isolations (i.e. idealisations and abstractions). They are constructed by way of rearranging and modifying the available conceptualisations of relevant and related phenomena. Moreover, we have seen that rearrangement and modification have a conjectural component in models of unintended social consequences. The combination of the isolated ele- ments in the model is essential. For example, we have not seen something like the chequerboard city before. By way of combining certain individual mecha- nisms (see Chapter 4), Schelling suggests that his initial intuition may be true. It is due to the familiarity of the individual mechanisms presented in the model that we tend to think what happens in the chequerboard city may happen in the real world. The initial hypothesis that residential segregation may be an unin- tended consequence is a conjecture and the chequerboard model shows that it is a plausible conjecture. More generally, models of unintended social phenomena embody familiar elements, what we have called individual mechanisms, and it is the interaction of these mechanisms that produce the unintended consequence.27 The similarity between these models and the real world consists in depicting some familiar mechanisms in isolation from others. Economising action and discrimi- natory preferences are such mechanisms. We know that these mechanisms exist. Models that characterise social phenomena as unintended consequences demon- strate a possible way in which they may interact and may produce certain results under certain conditions. If you like, we may call these individual mechanisms ‘tendencies’ or ‘capacities’ (Cartwright 1999). These models show us how those tendencies may work together (see the next section).

Figure 7.3 The chequerboard model.
We have seen that two conditions must be satisfied by explanations: the expla- nation has to be valid in the model world in order to render the initial hypothesis plausible, and the explanatory model has to be similar to the real world in certain respects. When these two conditions are met we get plausible conjectures about the way in which certain individual mechanisms may interact in the real world. These models alert us to some of the possible ways in which these mechanisms may interact in the real world. Let us explore these ideas further by way of dis- cussing some of the prominent views on models and theories.
Source: Aydinonat N. Emrah (2008), The Invisible Hand in Economics: How Economists Explain Unintended Social Consequences, Routledge; 1st edition.
