In Part I we argued that rates of founding and entry in organizational populations are much more complicated than birth rates in biotic popula-tions. In particular, we proposed that organizational founding and entry rates respond to processes of competition and legitimation. According to our model, levels of competition and legitimacy vary with the number of organizations in the population and with environmental conditions. The theory presented in Chapter 6 implies a particular form of non-monotonic density dependence in founding rates. That is, it implies that the founding rate rises initially and then falls with increasing density. This hypothesis is pivotal to our analysis because it implies that entry into populations of organizations does not mimic biotic birth processes, with their monotonie density dependence. Thus it is important to learn whether rates of founding and entry vary with density and whether such dependence has a nonmonotonic form. If it does, we can infer that opposing effects of legitimation and competition on founding rates contribute to the apparent stability of numbers in organizational populations.
In Chapter 6 we introduced our model of density dependence in founding rates. This section compares this model with other simpler models of the process that we use as baselines in evaluating goodness of fit. An organizational founding process (at any level of analysis) can usefully be considered an instance of an arrival process, one kind of point process. As described in the previous chapter, arrival processes characterize the stochastic behavior of the flow of arrivals to some state, such as events of radioactive decay, arrivals to a waiting line, events of cell division, and births. We denote the cumulative number of foundings (or entries, depending on the application) by time t with the random variable B(t).
The natural baseline model for arrival processes is the Poisson process (discussed in the third section of Chapter 8). Recall that the Poisson process assumes that the rate of arrival is independent of the history of previous arrivals, including the number of previous arrivals and the time of the last arrival. If the rate at which organizations enter a population follows a Poisson process, then the rate of founding or entry is a time- independent constant.
The Poisson process does not seem to be a plausible substantive model. If our theoretical arguments are correct, founding rates vary in response to changes in density and environmental conditions that affect carrying ca- pacities. Therefore, we concentrate on models in which the rate varies in some explicit way with observed covariates. The first part of our modeling effort was devoted to specifying density dependence and environmental effects. We began with the simple and classic Yule process often used to model phenomena for which each element can be assumed to have the same probability of producing a “birth” in a period, such as radioactive decay and growth in bacterial populations. The Yule process assumes that the per capita rate of founding or entry is a constant:
(9.1) λ(t) = cNt
where Nt denotes the number of elements in the population at time t. Note that this model assumes that the rate varies with the number of entities in the population rather than with the cumulative number of arrivals. In our applications the number in the population does not usually equal the number of previous arrivals because of mortality—organizations disband, they merge with other organizations, and they undergo radical change leading to exiting the population.
Inspection of data on organizational foundings and entries suggests that the per capita founding rate is not constant. Instead, the rate appears to rise initially and then to slow at higher densities. Therefore, in order to build a plausible baseline model of monotonie density dependence, we relax the assumption of constant per capita rates of founding and entry. We do so by using a generalized Yule model:
Dividing both sides of equation (9.2) by Nt shows that the per capita rate, λ(t)/Nt, varies with Nt in this generalization of the Yule model. Depending on the value of a, several kinds of qualitative density dependence are possible. If a – 1, this model is identical to a Yule process. If a > 1, the rate rises at an increasing rate with density; if 0 < a < 1, the rate rises at a decreasing rate with density. Finally, if a < 0, the rate falls with density.
We begin empirical analysis in the next section with a version of the generalized Yule model in which the constant c is replaced by a log-linear effect of a set of observed environmental covariates and period effects:
where xt represents a vector of environmental conditions measured at time t and Φp are a set of period-specific effects. In this model the founding rate varies in response to density, levels of measured environmental conditions, and shifts between periods chosen to represent qualitative changes in the social structure impinging on the population. Since this appears to be a plausible model of density dependence in rates of founding and entry, we use it as a baseline against which to assess the fit of our non-monotonic model.
Our theory of competitive and institutional processes implies that there is positive density dependence at low densities but negative density dependence at high densities. Thus we expect the rate to rise with increasing density to some critical level (the carrying capacity) and then to decline with further increases in density, assuming that the appropriate environmental conditions have been controlled. In contrast to the logic of the generalized Yule model, we predict that the effect of density on the rate is non-monotonic.
In Chapter 6 we specified our theory in terms of the following model:
with the prediction,
(9.4b) a > 0, y < 0.
Because of the log-linear form of (9.4a), the founding rate never equals zero in this model. Thus this model cannot imply a carrying capacity in the usual sense that growth rate of the population is zero. Nonetheless, if the parameters have the signs predicted by our theory (expressed in 9.4b), the founding rate begins to fall at some level of density and approaches zero at high densities. If the decline is rapid within the observed range of density, something like a carrying capacity exists. We explore such effects qualitatively in discussing our findings.
But the number of organizations in the population alone does not tell us the strength of competitive processes; we also need to take into account the environmental conditions that control variations in the resources over which competition occurs. Assume that some such conditions can be identified and measured. Then, in parallel with our specification of the generalized Yule model, we assume that the rate of founding or entry rate depends on the level of these environmental conditions and on a set of period- specific effects:
where xt denotes the set of measured environmental characteristics and Φp are a set of period-specific effects, as in (9.3). Of course, the set of relevant environmental variables depends on the population under study and the social/historical context. We discuss the measurement of such environmental variables and the choice of periods in the course of describing each empirical study.
In addition to investigating effects of density and environmental conditions, we also consider rate dependence, the possibility that the founding rate or entry rate in a population depends on the number of recent foundings and entries. Delacroix and Carroll (1983) analyzed rate dependence by estimating a quadratic relationship between prior foundings and the number of foundings in a year. We use a related specification for the effect of prior foundings (B) on the rate:
with the hypothesis that a wave of foundings increases the rate but that a very large number of recent foundings exhausts the supply of unclaimed resources needed to build new organizations. That is, we hypothesize that the effect of recent foundings is also non-monotonic, that
The last topic we investigate concerns links between populations. We begin with the model in (9.6a) as a representation of the founding process of a population in isolation, that is, when the other population is absent. Then we add two cross-effects, the first-order and second-order effect of the density of the second population:
where i and j denote the two populations. In this model the parameters αi and γi tell the effect of “own density” on the rate; the parameters θ1i and θ2i tell the cross-effect, the effect of “other density.” The cross-effect of density captures the effect of interpopulation competition. When populations compete in attempting to mobilize resources, the cross-effect of density will be negative for both populations. However, it is not obvious to us whether such effects are likely to be monotonie or non-monotonic; therefore, we explore both possibilities.
In developing qualitative implications of these models, we use the fact that their multiplicative structure allows them to be expressed as a product of several terms. When focusing on the effects of density, we refer to the multiplier of the rate due to the effect of density. For example, equation 9.6a can be written as:
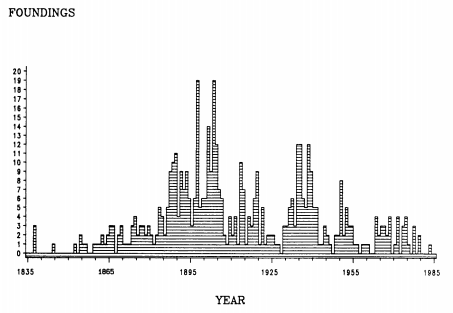
Figure 9.1 Labor union foundings by year
The expression immediately to the right of the equal sign, 
, tells the effect of density on the rate. In order to calculate the founding rate at any level of density, one evaluates this term for the level of Nt using the estimated parameters and then multiplies the result by the rest of the model. So we call this term that tells the effect of density the density multiplier. Similarly, we refer to 
as the multiplier effect of prior foundings. In order to learn about the qualitative behavior implied by our estimates, we plot estimated multipliers against density and number of prior foundings or entries.
Source: Hannan Michael T., Freeman John (1993), Organizational Ecology, Harvard University Press; Reprint edition.