Although a number of possible applications of the model suggest themselves (e.g., in the area of tax policy), most of these are best deferred until the model has been subjected to empirical test. However, departures from profit-maximizing behavior that are said to exist in the operations of public utilities are captured so nicely by our model that it may be worthwhile to develop them.
The rates a public utility is permitted to charge are set at levels intended to allow the utility to cover its costs and earn a fair rate of return. Ordinarily rates are not adjusted continuously as conditions change but are revised only periodically. In the short run, therefore, a utility may earn above or below normal profits but this is not a situation that will continue for very long; profits will eventually be restored to a fair level by rate adjustments.
Since above-normal profits can not long continue and since supernormal profits may invite the early attention of the regulatory commissions, the management of a public utility that has other than profit-maximizing objectives has an incentive to hold profits at or below some “safe” level. This tendency to absorb profits is further reinforced by the fact that the penalty for inefficient operations is particularly weak among the regulated monopolies. Not only is there a virtual guarantee that rates will be set to cover costs and permit the utility to show earnings sufficient to attract new capital; in addition, the regulatory commissions have not attempted to control costs. Hence, there is a positive reward for absorbing profits without an offsetting penalty. This situation is said to be responsible for the conditions of excessive staff and excessive managerial accommodations among the public utilities.
By inserting a maximum (or safe-level) profit constraint into the behavioral model, this sort of behavior can be shown to follow as a direct implication. Thus the objective is to
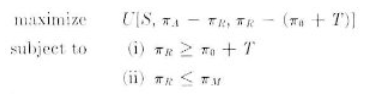
where π M = maximum safe level of profits to report.
By hypothesis, the minimum profit constraint is ineffective but the maximum profit constraint may be encountered. When this occurs, π R = π M and this can be handled by substituting π M for π R in the objective function. The problem then is reduced to
![]()
but the last term in this expression is a constant. Hence, the only terms that are relevant for maximization purposes are the staff and management slack absorbed as cost terms. Thus, the effect of encountering a safe-level profit constraint shifts the firm all the more into excessive staff expenditures and excessive managerial accommodations, which are indeed the implications we were looking for.
This sort of behavior need not be limited to public utilities, of course. Any firm which, for whatever reason (e.g., to discourage entry), finds itself encountering a maximum safe-level profit constraint could be expected to exhibit this behavior.
Source: Skyttner Lars (2006), General Systems Theory: Problems, Perspectives, Practice, Wspc, 2nd Edition.
