In the basic framework of chapter 2, we have assumed that the uninformed party has all the bargaining power and makes a contractual offer to the privately informed agent. In the case of common value, i.e., where the principal’s utility function depends on the state of nature (V = S(q, θ) − t), let us now flip the roles of these two players and assume that the privately informed player makes the contractual offer. To avoid the difficult issues of signaling,3 we assume that the informed prin- cipal makes his contractual offer before he learns the state of nature b. The timing of this ex ante contracting is shown in figure 9.1.
Figure 9.1: Timing of Ex Ante Contracting with an Informed Principal
The principal now has a utility function V = S(q, θ) — t for which we assume that the Spence-Mirrlees property Sqθ(q, θ) < 0 is satisfied. The agent gets a payoff U = u(t — θq), where u(.) is some increasing and strictly concave utility function (u‘ > 0, u” < 0 with u(0) = 0). As usual, θ belongs to 
with respective probabilities v and 1 — v.
According to the revelation principle, there is no loss of generality in restricting the principal to offer direct revelation mechanisms of the kind 
. For further references, we denote the principal’s information rents in both states of nature by 
. As usual, we can replace the menu of contracts 
by the menu of rent-output pairs 
to perform the optimization of the principal’s problem.
The principal being informed of his type ex post, any contract that he offers at the ex ante stage must satisfy the following incentive constraints of the principal:
where 
. Because of the assumptions made on S(.), Θ(.) is an increasing function of q. Summing these two incentive constraints and using that Θ'(•) > 0, we obtain the monotonicity condition
Moreover, because the contract is offered at the ex ante stage, the risk-averse agent’s ex ante participation constraint is written as
Expressing transfers as functions of the principal’s information rents V and V¯, we obtain
In what follows, we can neglect the principal’s ex ante participation constraint, because the principal has all the bargaining power at the ex ante stage when the contract is offered. The principal’s problem can be written as
Indeed, the principal must maximize his ex ante payoff subject to the agent’s participation constraint and to his own incentive constraints, ensuring that ex post, i.e., once he has learned the state of nature, he will truthfully reveal this state of nature.
Symmetric Information
As a benchmark, let us ignore for a while the incentive constraints (9.1) and (9.2) and solve for the optimal contract under symmetric information. This contract requests efficient production for both types, i.e., 
. Moreover, this contract provides full insurance to the risk-averse agent. Formally, we must have
Figure 9.2: First-Best Contracts with an Informed Principal
The Spence-Mirrlees property Sqθ < 0 ensures that the monotonicity condition always holds for the first-best outputs, i.e., 
. In order to make the problem interesting, we assume that the incentive constraint (9.2) is not satisfied by the first-best allocation. Using (9.6), this occurs if 
, which holds if
We have represented the optimal first-best contracts A∗ and B∗, offered in the states of nature θ and θ¯, respectively, in figure 9.2. Note that the Spence- Mirrlees property Sqθ < 0 ensures that the indifference curve of the θ¯-type crosses the indifference curve of the θ-type only once and then has a lower slope, as in figure 9.2. A higher level of utility is obtained when the isoutility curve moves in the southeast direction.
Asymmetric Information
Let us move now to the case of asymmetric information, where only P knows the value of b. By moving from B∗ to A∗ when state θ¯ realizes, the principal can increase his expected profit. On the contrary, the principal never wants to offer B∗ when he should offer A∗ in state θ.
The previous analysis suggests that (9.2) is the relevant incentive constraint in problem (P) when (9.7) holds. Denoting the multipliers of (9.2) and (9.5), by λ and μ, respectively, and optimizing with respect to V and V¯ yields
where the index IP means informed principal.
Summing these two equations, we obtain
where 
are the agent’s payoffs in the different states of nature. Hence (9.5) is necessarily binding at the optimum.
Lastly, we have
Because u(·) is concave, λ is positive if and only if 
.
Optimizing (P) with respect to outputs yields the second-best outputs, which are such that 
, and
We can summarize our findings in proposition 9.1.
Proposition 9.1: Assume that the agent is strictly risk averse and that the informed principal makes the contractual offer at the ex ante stage. Then, the optimal contract entails the following:
- Both the principal’s incentive constraint in state θ¯ (9.2) and the agent’s ex ante participation constraint (9.5) are binding.
- No output distortion for the production that is obtained when θ¯ realizes
.
.- An upward distortion for the production that is obtained when θ realizes , where
To understand the results of proposition 9.1, note that the principal’s incentive constraint (9.2) in state θ¯ is more easily satisfied when V¯ increases, V decreases and q increases with respect to the symmetric information optimal contract. Since only the incentive constraint (9.2) is binding, there is no need to distort the pro- duction when state θ¯ realizes. Under complete information, full insurance of the risk-averse agent requires zero profit for the agent in each state of nature. Under asymmetric information, the agent now receives a negative (resp. positive) payoff when θ¯ (resp. θ) is realized. Doing so increases (resp. decreases) the informed principal’s payoff V¯ (resp. V ).
These results are represented graphically in figures 9.3a and 9.3b. Keeping the same outputs as under symmetric information but decreasing (resp. increasing) the principal’s payoff when θ (resp. θ¯) realizes, the principal could offer the incentive compatible menu of contracts (A, B).
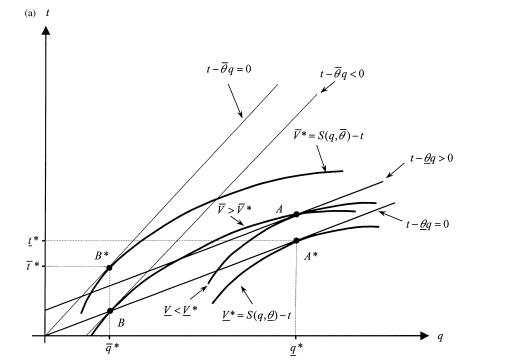
Figure 9.3a: Incentive Compatible Contracts with an Informed Principal
Figure 9.3b: Second-Best Contracts with an Informed Principal
This menu is incentive compatible because the principal is indifferent between contracts A and B in state θ¯ and strictly prefers A to B in state θ. How- ever, this menu imposes too much risk on the agent, who gets a negative payoff when θ occurs and a positive payoff when θ¯ realizes instead. Slightly increasing t¯, i.e., moving from B to BIP , while moving from A to AIP on the indifference curve of the principal in state θ¯, which goes through BIP , decreases this risk to the first-order and still preserves incentive compatibility (see figure 9.3b). Doing so only creates a second-order efficiency loss, because q∗ is maximizing allocative efficiency. This distortion is finally optimal for the pair of contracts (AIP, BIP).
Starting from the analysis above, it is useful to stress two important limiting cases.
Risk Neutrality
Let us assume that the agent is risk neutral and has utility function u(x) = x for all n. Then u'(x) = 1 for all x, and (9.11) suggests that λ = 0. Indeed, with risk neutrality, the first-best outcome can still be implemented by the informed principal.
To see that, consider the following information rents of the principal:
It is easy to check that (9.1), (9.2), and (9.5) are all satisfied by these infor- mation rents of the principal. As a result, the principal’s incentive constraints do not conflict with the agent’s participation constraint when contracting takes place ex ante and the agent is risk neutral. Juxtaposing this insight with the result of section 2.11.1, we can conclude that ex ante contracting never entails any alloca- tive inefficiency when both agents are risk neutral, whatever the allocation of bargaining power at the ex ante contracting stage.
Infinite Risk Aversion
Let us now assume that the agent is infinitely risk averse below zero wealth and risk neutral above. The ex ante participation constraint (9.5) is now replaced by a pair of ex post participation constraints, one for each state of nature:
Obviously those two constraints are binding at the optimum of the principal’s problem. Inserting the expressions V and V¯, which are obtained when (9.16) and (9.17) are binding, into the principal’s objective leads to the reduced form of the principal’s problem:
(9.18) is the principal’s incentive constraint when θ¯ is realized, i.e., (9.2) when V and V¯ have been replaced by their expressions obtained when (9.16) and (9.17) are binding.5
The solution to this problem is easy to obtain. There is no output distortion when θ¯ is realized, and again 
. Alternatively, there is an output distortion when b is realized. Since (9.7) holds, and since 
is decreasing over the interval [q∗, +∞], the incentive constraint is satisfied for a whole interval of outputs q in [qIP , +∞], where qIP is defined as
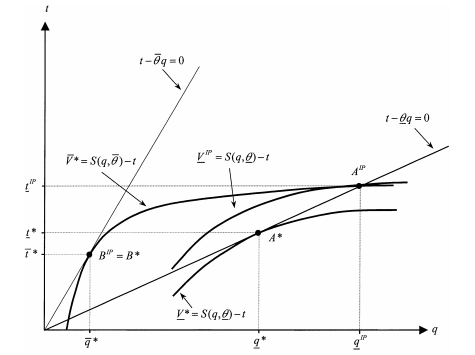
Figure 9.4: First-Best and Second-Best Contracts with an Informed Principal and an Infinitely Risk-Averse Agent
We can easily check that qIP > q∗. Because qIP > q∗, allocative efficiency is maxi- mized over the interval of incentive compatible outputs by picking qIP .
This distortion is represented graphically in figure 9.4, where we see that the full information contracts A∗ and B∗ lie on the zero-profit lines of the agent for each possible realization of the state of nature. For these contracts, the zero-profit lines are tangent to the principal’s indifference curves in each state of nature. Under asymmetric information, the inefficient principal still receives the alloca- tion B∗. The efficient principal instead over-consumes the good and chooses con- tract AIP . The corresponding output lies at the intersection between the principal’s first-best indifference curve in state θ¯ and the agent’s zero-profit line when b real-izes. This allocation ensures incentive compatibility, because the principal strictly prefers AIP to B∗ in state θ and is indifferent between those two allocations in state θ¯. Moreover, qIP is the output closest to q∗ on the zero-profit line of the agent in state θ, such that the principal’s incentive compatibility constraint in state θ¯ remains satisfied.
Remark 1: The reader who is knowledgeable in the theory of signal- ing will probably have recognized the similarity between the second- best outcome obtained above with the so-called least-costly separating equilibrium of signaling games. Indeed, let us consider the follow- ing game. First, the principal learns the state of nature θ, second, he chooses a “capacity of consumption” q, and third, a competitive market of sellers, the “agent,” offers the good to the principal up to his consumption capacity. One can show that this game has differ- ent classes of perfect Bayesian equilibria: pooling equilibria where the principal chooses the same capacity in each state of nature and sepa- rating equilibria where those capacities are different. Separating equi- libria thus reveals the private information learned by the principal to the competitive market. We leave it to the reader to check that those latter equilibria entail over-investment in capacity by the efficient type in order to credibly commit to signal his type to the market.7 More- over, the Cho-Kreps intuitive criterion selects the least-costly separating allocation from among these equilibria, which is precisely the alloca- tion that is obtained when the principal chooses q¯IP in state θ¯, exactly as under ex ante contracting (Cho and Kreps, 1987). In our model, the inefficiency of some equilibria of the signaling game can be over- come by writing an ex ante contract. However, not all inefficiency disappears even in this case, because incentive compatibility must be preserved.
Remark 2: The allocative inefficiency obtained above is strongly linked to the assumption of common values. Suppose instead that θ does not enter into the agent’s utility function, which is thus written as U = t − q for t − q ≥ 0, −∞ otherwise. Then, it is easy to check that 
implement the first-best productions. To have inefficiency, we must be in a common value environment.
The literature on informed principals is relatively thin but complex. Myerson (1983) and Maskin and Tirole (1990, 1992) are interested in models with ex post contracting, i.e., models where the principal offers the contract to the agent once he already knows the state of nature. These mod- els belong to the realm of signaling theory. Maskin and Tirole (1990) offer a noncooperative analysis of the game with private values. They show that the principal’s private information had no value in the case of quasi-linear utility functions. With risk aversion, they also show that the perfect Bayesian equilib- ria of the game are obtained as Walrasian equilibria in an exchange economy among the different types of principal. Maskin and Tirole (1992) analyze a game with common values and show that the perfect Bayesian equilibria of this game could be easily obtained as contracts giving higher payoffs to each type of principal than what they get in the least costly separating alloca- tion.8 Taking a cooperative perspective, Myerson (1983) shows an inscrutabil- ity principle, arguing that the principal could always build the revelation of the agent’s type into the mechanism itself. He goes on, presenting various concepts of solution, some of them being rather cooperative. Stoughton and Talmor (1990) compare the signaling and the screening distortions in a model of transfer pricing. Finally, Beaudry (1994) analyzes a mixed model where the principal privately knows the distribution of outcomes that the agent may gen- erate by exerting a nonobservable effort. He shows that an informed principal may be willing to leave a rent to his agent, even if the latter is risk neutral, just to signal his information on the technology. Interesting applications of the informed principal framework also arise in the industrial organization lit- erature. In Aghion and Bolton (1987), for instance, a supplier/principal wants to signal a low probability of entry to his buyer/agent by specifying inefficient damages for breach of the exclusive contract. See also Aghion and Hermalin (1990) and Spier (1992) for related arguments
Source: Laffont Jean-Jacques, Martimort David (2002), The Theory of Incentives: The Principal-Agent Model, Princeton University Press.