The attempts to examine the process of the emergence of money may be classified under three headings: computer simulations, experiments and theoretical models. First, ‘simulations’ and ‘experiments’ are examined, for they are directly related to the Kiyotaki–Wright (1989) model. Next, the theoretical models of the process of the emergence of money are examined, two of which are essentially different from the Kiyotaki–Wright model.
1. Simulations
Marimon et al. (1990) examine how individuals would learn to coordinate, or whether they would be able to coordinate in the Kiyotaki–Wright (1989) environ- ment. They replace the rational agents of the Kiyotaki–Wright environment with artificially intelligent (AI) agents. They examine whether AI agents would play fundamental strategies, or speculative strategies. To do this they consider different exemplifications of the Kiyotaki–Wright model, by considering different model economies with different specifications. It should be emphasised here that these simulations do not directly test hypotheses H(1) and H(2), but indirectly test them by testing the results of Kiyotaki–Wright (1989).
Marimon et al.’s AI agents can learn from experience and update their expecta- tions and strategies, given the information about their history. They are endowed with Holland’s (1975) classifier systems. A classifier system can be considered as a repertoire of behavioural rules or strategies for an individual.15 Obviously, for different situations different repertoires of strategies are applicable. However, only two decisions are important in Marimon et al. (1990): trading decision and consumption decision. We have seen above how trading decisions are taken. Indi- viduals are matched in pairs randomly, they simultaneously offer their goods, and decide whether or not to accept the trade offer. We know that they always accept their consumption good. But if they are not offered their consumption good, they have to decide whether to accept a good that they cannot consume. Many behav- ioural rules may be applicable to such a situation, such as ‘always accept trade’, ‘accept if the storage costs are low’, ‘accept if the storage cost of the offered good is lower than storage cost of the good in inventory’, ‘accept if other agents accept’, and so on. Two types of AI agents are examined in Marimon et al. (1990). The first type knows all the available strategies in advance. The second type knows only a portion of the available strategies, which is randomly assigned. Both types of agents attach strengths to every behavioural rule, or strategy, and update these strengths according to what happens when a certain rule is used. We may assume that the first time they trade, agents use one of the available strategies randomly, and if the randomly selected rule is successful, the agents increase its strength; if it is not, they decrease it. That is, every agent keeps track of the success of the available strategies they have executed. The classifier systems of the second type of agents evolve in a similar manner. However, in this case a ‘genetic algorithm’ is introduced to the system. Roughly, after some time, unsuccessful ‘classifiers’ die and new ones are introduced into the system, which are similar to the successful classifiers. The process of updating the repertoire of behavioural rules includes four operations: ‘creation’, ‘diversification’, ‘specialisation’ and ‘generalisation’. That is, occasionally new rules are added, modified, updated (to make them more specific to certain situations) and generalised. Generalisation is a genetic algo- rithm that occurs randomly (but the probability of its occurrence decreases in time) in the following way. Occasionally ‘rules’ are classified into two different groups according to their ranking (‘fitness’) among classifier systems: ‘potential parents’ and ‘potential exterminants’. Then, two ‘potential parents’ are randomly matched to create a ‘child’ rule, which has a strength equal to the average of its parents’ strengths. And each time a new child is created, a randomly chosen ‘po- tential exterminant’ dies. Given these characteristics, we may call the first type of agents as agents with ‘full strategies’ (F), and the second type of agents as agents with ‘random-partial strategies’ (R).
The results of Marimon et al.’s simulations are summarised in Table 6.2. The rows of the table summarise the specifications of different models used in the sim- ulations. Production columns show the production of different agents (remember that agent type i consumes commodity i). Storage costs columns show the storage costs of every good for different economies. The utility column shows the utility of consuming commodity i. ‘Initial CS’ column shows the chosen type of agent in terms of classifier systems: F or R. The last column shows the type of equilibrium reached by the agents after the execution of the simulation. F indicates that the simulation converged to the ‘fundamental equilibrium’, and S indicates that the model economy converged to a ‘speculative equilibrium’. A question mark, ‘?’, denotes that the simulation is not conclusive. The results of the simulations are shown in Table 6.2.16
For model economies A.1.1 and A1.2 the simulation converges to the funda- mental equilibrium, that is, AI agents learn to play fundamental strategies and commodity money emerges. In B1, the short-run behaviour of the simulation is close to the speculative equilibrium of the Kiyotaki–Wright model, yet in the long run AI agents learn to play fundamental strategies. For all other model specifica- tions the simulations are inconclusive, but Marimon et al. report that the results are closer to the fundamental equilibrium than to the speculative equilibrium. Concerning fiat money (economy C), Marimon et al. find that if the storage costs of real commodities are sufficiently high, and if a sufficient number of agents are endowed with the fiat good in the initial stage, and if agents do not know all of the available strategies (i.e. economy C2), then we may expect the economy to converge to the fiat money equilibrium. On the other hand, simulation results are inconclusive for economy C1.

Briefly, Marimon et al. (1990) test Kiyotaki and Wright’s insights, and con- clude that the fundamental equilibrium is more likely to be selected. In addition, Marimon et al. show that although not every model economy (e.g. models with different specifications and assumptions) converges to a monetary equilibrium, when the economy converges it is more likely that the good that is less costly to store emerges as a medium of exchange. On the other hand, the simulation fails to show that fiat money may be considered as an unintended consequence of human action, because there is no reason for the agents to hold a fiat good and use it in their exchanges – unless this assumption is made.
An important characteristic of Marimon et al.’s work is that it does not use a traditional analytical model to analyse the problem of the emergence of money. Instead the authors simulate the behaviour of artificially intelligent (AI) agents in different model worlds (e.g. economy A, B under different parameter values) and observe the agents’ behaviour with the help of a computer. This strategy helps the researcher to observe what happens (the process) under particular states of the model.17 Simulations usually show what is possible given the assumptions and specifications of the particular models used for the simulation. Briefly, Marimon et al. (1990) test Kiyotaki and Wright’s results with an artificial experiment. As with every experiment, these results are specific to certain model specifications (i.e. artificial laboratory conditions). In this way, they suggest that although the speculative equilibrium is a possible state of the model economy, it is less likely to be reached.18 For Marimon et al.’s results are valid for particular specifications of ‘the model world’, they partly support hypothesis H(1) – that commodity money may be an unintended consequence of human action – and cannot be argued to support H(2).
Gintis (1997: 24) argues that it is indeed true that Marimon et al.’s results are sensitive to the choice of parameters for the Kiyotaki–Wright (1989) model and he (1997, 2001) presents an alternative simulation.19 His simulation is differ- ent in that it is based on Darwinian notions, such as natural selection, mutation and adaptation, and it dispels AI agents. Gintis argues that both fundamental and speculative equilibria are possible (i.e. H(1) is supported), and that unless we assume at the outset that a very high percentage of agents accept a fiat good, a fiat good equilibrium will not emerge (i.e. H(2) is not supported). Gintis charac- terises the individuals as agents who are endowed with genomes that define their strategies, which evolve mimicking a Darwinian evolutionary process – that is, a process that selects the successful genomes (see Appendix II for a description of the model). Therefore, Gintis’s model does not give much role to the rational decisions of the agents. This may, of course, suggest that the emergence of com- modity money equilibrium does not need much intelligence or rationality. But since the model is characterised by the introduction of new agents who inherit the successful strategies of their parents, we may argue that that there must be some role for individual learning or imitation.
2. Experiments
A more plausible way to test these results is to conduct a ‘real’ experiment with real agents, rather than an artificial experiment. Such experiments have been con- ducted by Brown (1996), and Duffy and Ochs (1999). They examine the behav- iour of real individuals in the Kiyotaki–Wright (1989) environment. The question is whether the results of the Kiyotaki–Wright model hold if rational model agents, or Marimon et al.’s AI agents, are replaced with real individuals. Here, we will focus on Duffy and Ochs (1999) who have general a set-up where they consider different specifications of the Kiyotaki–Wright (1989) environment.20 In particu- lar, they inquire into the motivations of the real agents in such an environment.
In contrast to Marimon et al.’s artificial experiment, Duffy and Ochs (1999) conduct a ‘quasi-material experiment’ (see Morgan 2000), that is, they let the real individuals act in the Kiyotaki–Wright environment. The actions of the real individuals are constrained by the Kiyotaki–Wright environment, real individuals are supposed to act in an imaginary environment, and they are supposed to act according to the given specifications of the model world, and their behaviour is isolated from the effects of other factors by the model specifications. Yet the agents are real and Duffy and Ochs (1999) expect that their behaviour may help us in understanding whether the results of the Kiyotaki–Wright model and its variants may be carried to the real world. That is, they inquire what is possible in the real world. The conclusion of the experiment is as follows:
Our subjects showed a pronounced tendency to play fundamental strategies regardless of treatment conditions [. . .] At the individual level, behaviour reflected a response to differences in past payoffs – as assumed in reinforce- ment models, but did not reflect any response to differences in marketability conditions – as required by full rational Bayesian agents.
(Duffy and Ochs 1999: 873)
Duffy and Ochs’s experiment with human subjects supports Marimon et al.’s conclusion that agents are more likely to play fundamental strategies. Two conclusions follow from this: commodity money may emerge as an unintended consequence of human action (i.e. H(1) is supported), and real individuals do not play speculative strategies (i.e. Kiyotaki and Wright’s results concerning specu- lative equilibrium are not supported). Considering the first conclusion, we may say that this experiment takes the plausibility of the idea that ‘money may be an unintended consequence of human action’ one step further, for it shows that real individuals may bring about commodity money in an environment similar to that of the Kiyotaki–Wright model. Yet the results of Duffy and Ochs (1999) (as well as Marimon et al.) are valid for particular specifications of the Kiyotaki– Wright (1989) environment and there is nothing in this experiment that suggests that these results may be extended to more complex real-life situations. This also relates to the interpretation of the second conclusion: the specifications of the experiment may be responsible for the absence of speculative equilibrium. That is, although they show that the speculative equilibrium does not emerge in the Kiyotaki–Wright environment, this result does not necessarily apply to other en- vironments. This suggests that other experiments are necessary to see whether ‘marketability’ or ‘individual expectations’ are important in the process of the emergence of money.
Following this line of argumentation, Sethi (1999) argues that both fundamen- tal and speculative equilibria may be stable, and that the economy may evolve into these equilibria if agents are able to observe at least one strategy (and its success) other than their own. That is, it is argued that if agents are able to observe others’ behaviour and imitate them, they may end up in both kinds of equilibrium. Sethi argues that Duffy and Ochs’s experiment fail to test this idea for they only provide information about every individual’s own past payoff. He suggests an alterna- tive experimental set-up, where individuals may observe some other individuals’ performances:
An alternative experimental design, which could test both for convergence to speculative equilibria and for the propensity of individuals to respond to observed differences in payoffs, would provide each subject with his own average historical payoff as well as the average payoff obtained by the other players in the same sub-population. This could serve as a standard of com- parison that may induce players with below-average performance to experi- ment with alternative patterns of behaviour.
(Sethi 1999: 245)
Simply, Sethi suggests that the role of imitation and learning has to be examined further, both theoretically and experimentally, to get a better understanding of the process of the emergence of money. Yet imitation and learning are only examined theoretically in this literature and there is lack of empirical evidence. We now turn to the theoretical examination of the process of the emergence of money.
3. Theoretical models
Imitation
An evolutionary model which focuses on imitation is Luo (1999). Luo (1999) presents a model that emphasises the role of imitation in the process of the emer- gence of money. His model is based on the Kiyotaki–Wright environment, but there are three important differences. First, he introduces imitation to the model. Second, he assumes that all goods are perishable, and that they perish at the end of the day. Third, there are two trading sessions every day. Given these assump- tions, agents can exchange their production good with any good in the first trading session, but in the second session it is only rational to acquire their consumption good. Because of the absence of double coincidence of wants, it is rational for every individual to exchange their production good in the first period with a good that they may use to acquire their consumption good in the second period. When the trading sessions are closed every individual i meets another individual j with positive probability and if the agent j is more successful in acquiring his consump- tion good, i imitates j’s trading strategy with positive probability, and otherwise continue using the same strategy. Luo demonstrates that this process brings about one or many media of exchange. Different versions of the model (i.e. with dif- ferent specifications) are set to examine different questions about the emergence of money. The examination of these different versions show that storability (e.g. low storage costs) as well as the initial trading strategies (i.e. initial beliefs of the agents), the proportion of the agents who are specialised in producing different goods (i.e. relative number of different type of agents), and the amount of muta- tion (i.e. probability of agents playing arbitrary strategies) may determine the me- dium of exchange and the type of equilibrium (i.e. fundamental or speculative). That is, the initial conditions of the model determine the good that will serve as a medium of exchange. Moreover, there are more equilibria than there are in the Ki- yotaki–Wright (1989) model and several goods may serve as media of exchange at the same time, but if the mutation rate is sufficiently high the equilibrium that emerges out of the process of imitation is the fundamental equilibrium.
Obviously, this model is closer to Menger’s account of money for it takes into account ‘imitation’ in an explicit manner. Luo not only demonstrates that money may be considered as an unintended consequence in such a model world (i.e. H(1) confirmed), but he also explicates a possible mechanism that may bring about money. Briefly, he shows that Menger was right in suggesting that ‘imitation’ is an important mechanism in the process of the emergence of a medium of exchange. Yet by examining a restricted version of Menger’s account, he does not take us any closer to the real world.
Each and every model we have examined above is about coordination of indi- vidual activities. Yet the above models mainly focus on the problem of selecting the commodities that may serve as media of exchange. An alternative (but related) line of research explicitly focuses on the coordination of individual activities by way of abstracting from the selection of ‘candidate’ commodities that may serve as media of exchange. In this line of research two (or more) commodities are presupposed as candidate goods and individuals are supposed to face a coordina- tion problem: they have to select a good (or a combination of goods) to use as a medium of exchange. Roughly, individuals know that they have to use a good as a medium of exchange but they do not know which of the two (or many) goods would be used by others and would serve as a medium of exchange. So they have to focus on coordinating their behaviour.
Coordination
Schotter (1981) emphasises coordination and the role of learning from the history of play in the process of the emergence of money. He characterises individuals as agents who learn from experience and presents the problem behind the emergence of a medium of exchange as a coordination problem among agents in an agrarian society. (Schotter 1981: 35–39) It is assumed that there are no transaction costs, and that trade is mediated by a marketing agent. In this model economy there are m plastic chips (e.g. with different colours) that do not provide any utility to the farmers. Nevertheless, these chips are supposed to be used as media of exchange. When farmers come to the market they bring a number of chips that equals the equilibrium price of the goods they have supplied22 to the marketing agent, and they use these chips to buy goods from other farmers. The problem is that there is no uniform way to pay with these chips.23 For the market exchange to take place, every farmer has to decide in what chip or in what combination of chips he should be paid for, and in what chips he will pay for the goods he wants to buy. Thus, the farmers in the economy are confronted with a coordination problem. If two farm- ers cannot fully coordinate they can only exchange the goods that correspond to the number of chips they agree on. If they completely fail to coordinate they can- not trade. If, in time, all farmers coordinate on one type of chip, this chip emerges as the generally accepted medium of exchange. Of course, it may well be that the farmers coordinate on a mixture of chips, then this mixture of chips will function as the medium of exchange.
Let us present a highly simplified version of Schotter’s model. Assume that there are only two types of chips, A and B. The coordination problem facing the farmers every time they need to trade can be represented with the chip game in Table 6.3. If farmer I (seller) wants to be paid in As (i.e. plays A) and if farmer II (buyer) wants to pay in Bs (i.e. plays B), they cannot trade. Thus, we assume they receive zero payoffs. But if they are able to coordinate on either A or B, they will be able to trade and get what they want – hence the positive payoff, a. They have to make their choices simultaneously and they cannot communicate.
We have said that if both players choose the same option they have positive payoffs and otherwise they get nothing. That is, if they choose (A, A) or (B, B) they are able to coordinate. In game theory these two coordination points are called Nash equilibria. In a Nash equilibrium, the players’ strategies are the best responses to the other players’ strategies, that is, players get the highest payoff given others’ strategies (see Gintis 2000: 6–14; Bierman and Ferandez 1998: 16). Or more intuitively, ‘no player has any incentive to deviate unilaterally from it’, so ‘players do not regret their strategy choices’ (Colman 1995: 59). Of course, farmers see that it does not matter on what type of chip they coordinate, yet there is no way that they can know what the other will choose in advance (see Chapter 8). For this reason they may also choose to randomise their actions (i.e. play mixed strategies) in order to increase their chances of coordination. For example, they may play both options with equal probability.24 More generally, if farmer I and II meet for the first time in the market, they have no way of knowing the way in which the other will want to trade. Now, suppose that there are N farmers in the economy, and that they are randomly matched in pairs. In period 0 (i.e. the first time they trade) all farmers would face a situation similar to the one described for Farmer I and Farmer II. Assume that all farmers randomise their choices in period 0. In period I, farmers may reconsider their choices given what happened in period 0.This may happen in many ways,25 but Schotter assumes that all players are able to observe the behaviour of the rest, and that they all observe the same history. Given this assumption in every period, all farmers would revise their expectations about the likelihood of the choice of others given the information about the last period.26 For example, if the percentage of farmers who play A is 70 per cent in period 0, then in period 1 every farmer would expect others to play A 70 per cent of the time.27 The logic behind this is the following: ‘if it happens in the past, it is likely to occur in the future’ (Schotter 1981: 72).

In this model the history of play matters. In period 0, no-one knows what to expect from others, but as time passes the players update their expectations and increase their chances of executing a successful trade. If, eventually, all players expect A (or B) to be played by all the other players all the time, they will play A (or B) all the time and A (or B) will be established as a medium of exchange. Moreover, no-one will have any incentive to do anything else. Both equilibrium points, (A, A) and (B, B), are stable. Note that because of the probabilistic nature of the expectations, updating rule and strategies, the model is not deterministic. Either A or B may emerge as a medium of exchange. Both conventions, (A, A) and (B, B), are equally probable. At first sight, it seems that the players would end up coordinating on one of these options, for they may be locked-in to one of the options after some time. But the probabilistic nature of the strategies implies that there is always a chance that some players would choose the less likely option. For example, if the history of play dictates that A is played with 0.9 probability, there will still be players who may play B in the next period. Thus, to assume that the individuals update their expectations does not guarantee that the process will end up in a stable equilibrium – at least in a reasonable period of time.
Schotter makes an important assumption, meant to increase the likelihood that one of the equilibrium pairs is achieved at the end of the process. He assumes that if the state of the model is close enough to a state where every individual expects others to play a certain strategy with unit probability (e.g. they believe that 98 per cent of the farmers choose A), every farmer will behave as if they have expected every other to play with unit probability.
Normally there are two points, (A, A) and (B, B), where everyone would expect everyone else to play a particular strategy with certainty (see Figure 6.2a). Schot- ter call these ‘absorbing points’ because once they are reached no farmer would have an incentive to deviate. The additional assumption made by Schotter (1981: 99–100) tells that every individual would consider points close to (A, A) and (B, B) as absorbing points as well (see Figure 6.2b).28 That is, players are assumed ‘to use a particular pure equilibrium strategy as soon as the players all believe that’ a certain ‘strategy is very likely to be used’ (Schotter 1981: 100). Hence, if the ‘absorption area’ is large enough, we may expect a medium of exchange to emerge out of this process. Given this assumption, we learn from this model that if market-dependent, economising individuals are able to update their expectations about the others, it is very likely that they will coordinate their behaviour concern- ing the selection of a medium of exchange.
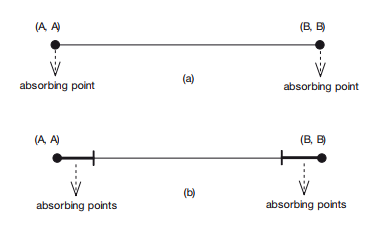
Figure 6.2 Absorbing points in Schotter (1981).
An important difference between Menger’s and Schotter’s explanations is that Schotter assumes at the outset that trade should be mediated by some intrinsi- cally valueless chips. The agents know that they are supposed to use a medium of exchange. For this reason, the model cannot explain the transformation of a world where the idea of a medium of exchange is non-existent to a world where individuals use a medium of exchange. Schotter only shows that coordination is possible. Yet he does not explain how the model economy came to a state where all individuals know that they have to use a medium of exchange. Hence, the emergence of a medium of exchange remains unexplained. To put it boldly, if one wants to explain the emergence of a medium of exchange, he or she cannot assume at the outset that individuals know that they are supposed to use a medium of exchange.
It is easy to see that Schotter’s model deals with a small part of Menger’s story. He does not have a theory of saleableness, he just assumes that plastic chips are used in trade – thus limiting the number of ‘candidates’ at the outset. He does not picture a process of discovery, but only a limited type of ‘inconclusive’ learning from past experience. As it is with the equilibrium models, Schotter shows that the existence of money depends on the common belief that it will be used by others in exchange, and that it is a possible state of the model economy. In addition to this, he demonstrates how a common belief may emerge from a trading environment where individuals are supposed to use a medium of exchange. For this reason, he fails to show that money may be considered as an unintended consequence of human action.
His analysis only makes sense as an account of the emergence of money if it is plugged into Menger’s account. Menger explains (in the model world) how indi- viduals may start considering using certain goods to acquire their needs through discovery, learning and imitation. Yet it is possible that at a certain stage in this process different groups of individuals use different goods to mediate their ex- changes. At such a state individuals may see the advantage of using a medium of exchange, but they cannot expect every other to accept the same good in their exchanges. This (possible) stage can be considered as Schotter’s starting point: there are a couple of goods that are known to be accepted by some, but not all. The individuals have to coordinate their behaviour on a certain type of commodity, and Schotter shows that this is possible if they update their strategies. Moreover, the assumption that if individuals are close enough to the absorbing points they will use pure equilibrium strategies can also be justified with Menger’s frame- work by saying that the increase in the use of a particular good in exchange would increase its marketability and, thus, after some time, individuals would consider that very good as a natural ‘candidate’ to use in their exchanges. When considered as a contribution to Menger’s account, Schotter’s model supports the idea that commodity money may be an unintended consequence of human action (i.e. H(1) supported). However, plugging Schotter’s account into Menger’s story would not make sense for the emergence of fiat money. Since individuals would neither hold a valueless good nor consider using it as a medium of exchange, Schotter fails to show that fiat money can be considered as an unintended consequence of human action (i.e. H(2) is not supported).
A similar account of coordination is presented by Young (1998: 11–16, 72–73), who uses the following currency game to demonstrate his general approach to coordination problems. Consider the game in Table 6.3 again. Schotter assumes that the players would use the information about the history of play to update their expectations. Yet he also assumes that only the information from the last period is relevant. Young (1998) suggests that it is more plausible to assume that individuals observe and remember more periods, but not all of them. In what follows, we present a highly simplified version of Young’s approach to present his main points.
Young assumes that individuals are boundedly rational and they can only observe a fraction of what happens around them. First of all, they have limited memory: if individuals have been trying to coordinate for t periods they could remember the last m periods and base their decisions for the next period on what happened in the last m periods (t > m). When there are n individuals, each indi- vidual observes what has happened in the last m periods, calculates the frequency distribution of As and Bs for this time period, and chooses a best reply to this distribution – that is, they try to maximise their expected payoffs, given this dis- tribution. Second, they have limited information. That is, in the n-player case every player is able to observe a fraction of actions of the other players: they may observe only s players’ actions (1 < s < n).29 Simply, if player i observes that A is more frequently played than B in the last m periods, then player i chooses A in the next period, because choosing A is expected to yield more utility.
Similarly to Schotter, Young shows that equilibrium points (A, A) and (B, B) are absorbing points (see Young 1998: 51) and that they are (stochastically) sta- ble.30 More precisely, assume that there are two players that can observe the last two periods. Let w denote the action of player I two periods ago, and x denote the action of player I in the last period. Similarly, let y denote the action of player II two periods ago, and z denote the action of player II in the last period. Then each player is able to observe the information string wxyz. Let us now assume that both players played A for the last two periods. Then the information string wxyz would look like the following: AAAA. If the players chose a best reply to this informa- tion string then they will have to choose A in the next period. This means that they will be responding to the same information string in the next period, and they will choose A again. Thus, when the model evolves to a state where AAAA (or BBBB) is observed, the model will stay in this state forever. Young also shows that from any initial state one of these goods (A or B) emerges as a medium of exchange with probability one.
But, of course, players may make mistakes, or some players may play in an idiosyncratic way, for example, for other reasons which are not considered in the model. In Young’s approach this is reflected by an error rate ε (ε > 0), which is small.31 That is, player i chooses a best reply to the frequency distribution with probability (1 – ε), and chooses an option (strategy) at random with probability ε. In this case, in the short run the best reply dynamics (the process of adaptive learning) will take the system to one of the Nash equilibria, (A, A) or (B, B), and it will stay there for a long period of Yet because of the random shocks (or the error rate), the system will not stay there forever. That is, if a number of errors occur in a line, the accumulation of these errors will carry the model from one equilibrium to the other. Young (1998: 12) argues that this may be considered as representing ‘shifts in economic and social norms’ after long periods of inertia (i.e. abiding to one convention for a long period). Briefly, his model shows that money is bound to emerge if individuals learn from experience, but in the long run social institutions may change if individuals change their behaviour for a sufficiently long period of time.32 Young (1998: 51–54) also shows that if coordinating on (A, A) yields a higher payoff than coordinating on (B, B),33 and if the error rate is positive, the equilibrium with higher payoffs, that is (A, A), will be selected and A will emerge as a medium of exchange no matter what happens in the initial stages. Briefly, the ‘superior’ good is more likely to emerge as a medium of exchange.
Young tries to show how individuals who have limited memory and informa- tion and are trying to get the ‘best trade’ at the moment may bring about a social institution, such as money, as an unintended consequence of their action. Yet our comments on Schotter (1981) also apply to Young. Although he does not explic- itly assume that there is a marketing institution as Schotter does, he supposes that individuals are willing to use a medium of exchange by assuming that their inter- ests coincide. For this reason, Young only shows that coordination is possible, and his model fails to explain the emergence of a medium of exchange. Yet plugging his model into Menger’s account gives us a better idea about the way in which a medium of exchange may be brought about.
Source: Aydinonat N. Emrah (2008), The Invisible Hand in Economics: How Economists Explain Unintended Social Consequences, Routledge; 1st edition.
