The following propositions about the behavior of firms are consistent with both an orthodox and an evolutionary view, although the emphasis and connotations of each would be different: at any time, firms in an industry can be viewed as operating with a set of tech niques and decision rules (routines), keyed to conditions external to the firm, prominently prices, and to various internal state condi tions, in particular the firms’ capital stocks. Expansion or contraction of firms is related to the profitability of such moves. Firms also may have procedures for hunting for better techniques.
In the orthodox formulation, the decision rules are assumed to be profit-maximizing over a sharply defined opportunity set that is taken as a datum, the firms in the industry and the industry as a whole are assumed to be at equilibrium size, and innovation (if it is treated at all) is absorbed into the traditional framework rather me chanically. In evolutionary theory, decision rules are viewed as a legacy from the firm’s past and hence appropriate, at best, to the range of circumstances in which the firm customarily fin ds itself, and are viewed as unresponsive, or inappropriate, to novel si tuations or situations encountered irregularly. Firms are regarded as expanding or contracting in response to disequilibria, with no presumption that the industry is “near” equilibrium. Innovation is treated as sto chastic and as variable across firms.
These differences in perspective mean that when analysis deals with the effects of changed market conditions upon behavior, the focus is on different things . The following analysis of the behavior of firms and the industry is at once general enough to encompass both perspectives and designed to highlight the differences.
Let xi be the vector of firm i’s outputs and variable inputs, the latter taken as negative. Assume for simplicity that the levels of inputs that are fixed in the short run can be represented by a scalar, ki, the size of the firm’s capital stock. And assume that firm i’s deci sion rule governing output and variable input levels has the follow ing general form :

Here P is the vector of output and variable input prices corre sponding to Xi , and di is a vector of decision rule parameters. (For notational convenience we treat all differences among alternative possible decision rules, among firms and over time, as parameter differences. )
In a behavioralist view, the complex multidimensional rule of equation (1) should be considered as a collection of simpler rules guiding particular input and output decisions, with the simpler rules regarded as but loosely connected. An orthodox view also admits a decomposition of the global rule into a collection of subrules, while ordinarily presuming strong linkages among these subrules.2 But from either perspective, it is legitimate to consider separately dif ferent kinds of subrules. Thus, in the customary textbook treatment, sometimes the focus is on the rules used by firms to determine vari able input and the analytic concern is with the mix among variable inputs used (with a given stock of capital) as a function of factor prices. Of course, in considering input mix rules, it must be under stood that output also may be varying as a function of input pri ces. It is customary to limit the analysis, at least at a preliminary stage, to the choi ce of a cost-minimizing input mix with output level constant. Sometimes the focus is on output decisions. Here Xi refers to an out-put, and the analysis relates to the nature of the firm’s rule con necting the quantity of output th at will be produced (given a capital stock) to output price. It is understood that variable inputs will (nor mally) rise as output rises. In strict logic, of course, the input and output levels of th e orthodox competitive firm are simultaneously de termined optimal values at each vector of prices for all inputs and outputs. In that context, the vector function D(‘) in equation (1) should be interpreted as expressing the general solution of that simultaneous equation problem, and the values of the parameters dt are the optimal ones. The generality of the formulation, in the ortho dox . perspective, is q ualified only by the fact that the solution is expressible as inputs and outputs per unit capital stock, which im plicitly assumes constant returns to scale and a unidimensional capital stock.
. Let X = ∑xi and let K =∑ki (all summations here are over the index i) , Then, for the industry:

Under any market regime X/K may evolve over time. The tradi tional comparative statics appro ach of price theory represses what happens to X/K over time for a given set of market conditions and fo cuses on the variation associated with different market conditions. In what follows, we will be explicit about both kinds of differences.
Consider two different market regimes. In regime zero, prices are at P0 forever. Under regime one, prices are at P0 until time t and at P1 after that time. Consider some time T greater than t. Then, under regime zero we can “account for” X/K at time T as follows :

The superscripts T and t identify the time at which the variables are measured. The subscript zero has been used to tag variables that may be different at time T under regime zero than under regime one. Given this notation, the first term is, of course, (X/K)t. The second term accounts for the effects of the evolution of rules between t and T, weighted by capital stocks initially (at time t). The final term ac-counts for selection effects that change capital share weights on the final rules.
Under regime one, X/K at time T can be accounted for as follows:

By subtracting equation (3) from equation (4) one can “account for” the difference in X/K at time T under the two market regimes.
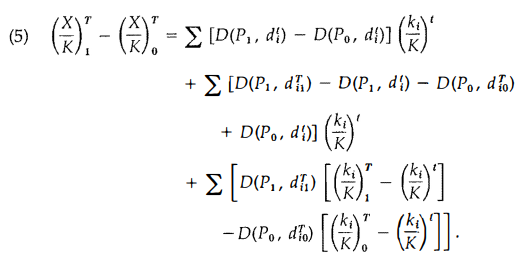
The first term (or, properly, the terms under the first summation) can be ‘ viewed as the result of firms’ moving along the decision rules at time t in response to a change in price from P0 to P1. The second term reflects the fact that decision rules may evolve differently under the two regimes. The final term accounts for the d ifference in selection effects.
The above decomposition of the diffe rence made by a price change could be regarded as merely a matter of accounting, without causal significance. We believe, however, that the separation we pro pose is useful analytically, because the three terms correspond to the operation of analytically distinguishable mechanisms. Thus, in what follows we will analyze separately along-the-rule effects, search effects , and selection effects of a change in price regimes. Although what is essential to the theorizing is that separable mechanisms are involved, we put forth as a tentative empirical proposition that the three e ffects occur at different speeds and that it is convenient to think of the along-the-rule effect as occurring promptly, followed by the appear-ance of differential innovation effects, followed in turn by differen tial selection effects . Our identification of the three terms in our par ticular accounting of distinct causal mechanisms rests on this image of the sequence of events. But our discussion of the individual mech an isms is relevant whether they are assumed to operate in this se-quence, some other sequence, or-realistically -concurrently.
In any case, the prototypical question of positive economic theory is: What is the sign of the difference analyzed in equation (5)- say, the sign of the response of intensity of use of an input to a rise in its price? In deference to tradition and the weight of empirical evidence, we shall call the results that accord with orthodox qualitative predic tions “standard” and results that fail to accord “perverse. “
Orthodox theory derives its “standard” results from the assump tion of profit maximization over a given choice set. In terms of the accounting framework above, orthodox theory may be interpreted as a theory about responses governed by decision rules. The second and third terms are not considered. Our analysiS involves both rejec tion of the orthodox view of the derivation of decision rules, and emphasis on the likely importance of the second and third terms. For overall industry response to be standard, it would be sufficient for each of the three terms in our accounting to carry the sign of standard response. We shall consider each mechanism in turn.
Consider the movements along prevailing decision rules, ac counted for in the first term. It is implicit in both the behavioralist and the orthodox notion of a “decision rule” linking input and out put quantities to prices that at any particular time there is a certain set of action alternatives open to the firm. For an orthodox economist this set is a technological “given” and the decision rule is derived by optimization over it. For us, the rules are what they are because they have evolved that way over time. The concept of known ” possible ac tions” has no standing independent of the actions invoked by deci sion rules. These rules are themselves observable (in principle) by looking “inside” the firm . Indeed, this may be the only way to actu ally find out what they are. Since some of the responses invoked by rules take time to work out, and since over time the rules may change, it is risky to try to infer rules from observed market responses that take place over time. In any case, under an orthodox interpretation of decision rules or under ours, it is implicit that if a firm takes one action under one market condition and another action under another market condition, it could have done exactly the re verse.
Given this interpretation, a prediction of a standard sign of along-the-rule change can be derived from the assumption that the rules reflect sensible profit-seeking behavior. The specific assump-tion is that routinized responses to price changes are not worse, in profitability terms, than no change at all. Let ![]() denote the full vector of input and output flows “per unit capital” under regime P0 . Holding the d ecision rule constant but changing the price,
denote the full vector of input and output flows “per unit capital” under regime P0 . Holding the d ecision rule constant but changing the price, ![]() . Treat k as a constant. Then (repressing both k and the i subscript) profit under regime one equals P1 . X1 > P1 . x0 , or else the firm would have done better to stick with X0 . Similarly, P0 . X0 ≥ P0 . X1. Familiar algebra yields the conclusion ΔP .ΔX ≥ O. Hence, if ΔP has a single nonzero component, the corresponding element of Δx . cannot carry the opposite sign from that component.
. Treat k as a constant. Then (repressing both k and the i subscript) profit under regime one equals P1 . X1 > P1 . x0 , or else the firm would have done better to stick with X0 . Similarly, P0 . X0 ≥ P0 . X1. Familiar algebra yields the conclusion ΔP .ΔX ≥ O. Hence, if ΔP has a single nonzero component, the corresponding element of Δx . cannot carry the opposite sign from that component.
Although the conclusion and its derivation are familiar and ortho dox, the interpretation is not. This is a hypothesis about decision rules, involving no commitments regarding the existence of an inde pendently specified set of “known” or “possible” production methods, or about the characteristics of the processes that introduced these methods in the firm and established the decision linkages between them and the prices. The argument rests on the assumption that Xo is an “available” behavior when PI prevails, and similarly for Xl and Po . The hypothesis is that the decision rules are plausibly re sponsive to changed conditions, not that they are”optimal” among the set of alI “possible” decision rules (whatever that might mean). To illustrate, consider again the decomposition of the global deci sion rules customarily employed in conventional textbooks. Thus, the analysis above can be speciali zed to refer to the proposition that, for a given quantity of output produced, a change in inputs induced by a change in input prices will be such that the cost of producing output at the n ew input prices is not increased . In the neoclassical analysis, changes in inputs reflect changed points of tangency of an isocost line with an isoquant; in our formulation, although changes in input proportions reduce unit costs, there is no underlying iso quant to which an isocost can be made tangent. Another common specialization, of course, is that a change in output price will induce a change in output in the same direction. Here the neoclassical analy sis presumes movement along a marginal cost curve, and our more general proposition does not.
The hypothesis that the along-the-rule response is standard cer tainly is not true by definition. There are several reasons why it might prove false. It could be that the firm does not consider chang ing its inputs in response to changing prices; then decision rule “response” would not be strictly perverse but it would not be strictly standard. It could be that the profit calculation does not adequately reflect the structure of the firm’s goals. For example, the firm (or rather its managers) might have a distaste for a relatively profitable act ivity that employs a particular input intensively, but might be bound by a minimum profit constrain t. Then a rise in the price of the input might, by decreasing the profitability of its current mix of activities, lead the firm perversely to undertake its disliked activity more intensively. It could be that there are minor errors built into the rules, that one behavior is employed when another is slightly more profitable ; or it could be that really major blunders are built in. How ever, the proposition that the routinized component of response to price change is standard seems likely to be of sufficiently broad validity to warrant its tentative acceptance as a theoretical commit ment . (For the purposes of equation (5), t he relevant question is whether the appropriately weighted average of routinized response is standard, so there is room for some exceptions. )
The second term of o ur accounting reflects the consequences of changes in decision rules under regime PI compared with what would have happened under Po . We use the term “search” as a ru bric for the variety of processes, mostly intentional but some not, by which rule changes take place . The question is: Will the effect of the changed price regime on search be standard?
Se arch differs from routinized response in three fundamental respects. First, inasmuch as it involves the acquisition of informa tion, it is intrinsically an irreversible process. The irreversibility is rooted in the familiar economic fact that the costs of retention and use of a given item of information are typically much lower than the costs of initial acquisition or production. An immediate implication of irreversibility is that a pred iction of a standard response of search outcomes to price changes cannot be derived by the same the oretical argument just used for the case of rule-governed response. Although it remains plausible that rule changes will tend to enhance profitability, t he re is no reason why the new decision rules yielded by search should not dominate the old, and be more pro fitable at the old prices as well as at the new.
The second fundamental characteristic that distinguishes search is uncertainty. The scene surveyed by a decision maker inside the firm may well include identifiable “alternatives” that could be explore d, but these are only dimly perceived and it may not be at all clear which will turn out to be best. The process of exploring perceived alternatives, or exoge nous events, may bring to light other alterna tives not even contemplated in the original assessments. As argued earlier, uncertainty and individual differences are structural aspects of search. It is clearly appropriate to conceptualize and model search as a stochastic process. And it is clearly inappropriate to apply uncrit-ically, in the analytical treatment of that process, formalisms that posit a sharply defined set of perceived alternatives, to which no behavioral reality corresponds.
Last, search is distinguished by what we may term its contingent character. Real search processes take place in specific historical con texts, and their outcomes clearly depend in part on what those con texts contain in the way of problem solutions that are available to be “found.” What there is to be found consists in large part of the fruits, by-products, and residues of information- producing activities else where in the society. The flow of general social history thus impinges directly on the firm through its search activities, and searching at t is not the same thing as searching at T > t.
We have probably exaggerated here the extent to which the con ceptual distinctions among irreversibility, uncertainty, and contin gency are clear-cut. Rather, these are three interrelated aspects of the single central fact that search processes are historical processes, not repetitive and not readily separable from other p roces ses of historical change. Awareness of that central fact should perform the valuable function of keeping the ambitions and pre tens ions of economic theorizing under realistic control; there is reason not to expect too much.
Distinguishing among the three characteristics is helpful in a more specific sense: it provides the basis for a taxonomy that clarifies the contribution and limitations of particular modeling approaches. For example, one approach to modeling the firm’s search for superior techniques involves taking input coefficients (or changes therein) as the objects of the search. This approach suppresses the contingent aspect of search at the outset; it loses contact immediately with the fact that the realities of search for techniques involves questions of improved machine design, work arrangement, and so on, and that answers or partial answers to such questions are generated by pro cesses external to the firm. But at the price of accepting this rather ex treme abstraction, we can construct simple models that illustrate the “tendency” for search outcomes to be deflected in the “standard” direction by input price changes. We shall demonstrate below that “standard” results are obtainable in a simple “search-and-test” model in which t he direction of search is not influenced by factor prices. A searching firm draws on a random distribution of tech nological coefficients in the neighborhood of its current techniques; it compares the cost of the alternative technique it “finds” with costs associated with the status quo, and it switches if the alternative is less costly. The distribution may be such that there is a coefficient drift in one direction or another under a wide range of factor prices. However, the e xpected c hange in input coefficients resulting from search is deflected in the standard direction by a change in relative input prices.
It is plausible, of course, to assume that input prices affect the search process in more subtle ways than merely by providing param eters of a test applied to a discovered result. For example, the ex pected gains from an array of different R&D projects may be reor dered by a change in prices so that the nature of what is attempted by the firm is changed. Th is too can be modeled, and the standard result may again be obtained. There are also relevant mechanisms traceable to certain descriptive regularities of behavior. Cyert and March (1963) advanced the generalization that organizational search is “problemistic” : it is stimulated by a particular problem, and the symptoms of the problem define a neighborhood in which the search takes place. If the “problem” is a profit reduction associated with the rise of a price of an input, and if the symptoms (cost increases) show up most vividly in certain activities or product lines that make inten sive use of that input, one might expect that the firm’s problem solving activities will be directed to those areas. It is also plausible that search will be structured by the question “How can we reduce our use of this input?” If a search process thus directed and struc tured is successful, it will probably reduce use of the input.3
So the hypothesis that price change- induced changes in search outcomes are standard is plausible. But proper interpretation of the hypothesis requires some delicacy. First, insofar as the model treats search (appropriately) as stochastic, the hypothesis necessarily re lates to “tendencies,” or average results. An individual outcome may eas ily be perverse. Second, since search may take place even in a constant market regime, the hypothesis about the consequences of a change in regime necessarily involves a comparison with “what might have been”-that is, the path of technique change that would have occurred under the original regime. There is no reason why search outcomes might not be strongly biased in one way or another, reflecting the relative ease or visibility of certain kinds of innova tions. For example, under some circumstances it may be that ways to save labor are obvious to see and easy to develop, relative to other kinds of innovation, and that the evolution of technology (decision rules) will show a labor-s aving bias under a wide range of possible factor price ratios. Under these circumstances, search may reduce labor input over time in a regime of constant wage rates, and lower wages would simply mean a slower drift in that direction than would higher ones.
Even when delicately posed, the hypothesis that the results of search are standard is not of self-evident validity; intelligent pro fit-seeking behavior does not n ece ssarily imply it. Consider, for example, the following scenario. A metal fa bricating firm confronts a sudden rise in the price of its raw material. It makes routine adjust ments to this change by, say, making greater use of odd-shaped pieces of material that were formerly treated as scrap. After this ad justment, a severe profit pinch remains, and triggers off a search for ways to deal with this situation-a search that would not have been undertaken had the price increase and cost crisis not occurred. The result of the quest is the discovery that new types of labor-saving machinery, adaptable to the firm’s problems, have become available. The firm buys such machinery and eases its profit problem – but the new machinery is less tolerant of odd- shaped pieces of material than were the workers who previously performed the relevant operations . As a result, the raw material intensity of the output increases. Search triggered by the price rise has contributed a perverse component to the total response of the firm . The decision rule change moved the firm in the direction opposite to that in which its routine decision rule moved it. Because search would have been less, the firm would not have discovered this decision rule change in the differe nt factor price regime.
The third term in the decomposition captures the effect of different price regimes on the growth or decline of firms that have dif ferent time T decision rules. Again, under a variety of assumptions selection effects will be standard. For example, assume that routin ized and search responses occur sufficiently rapidly so that capital shares can be considered as practically constant while these changes are going on. Then the reweighting effect is a pure selection effect on decision rules that have been established shortly after t and that are constant over the selection period . It can be shown that under these assumptions the selection effect of a change in the price of a single input is standard, if firm growth rates are linearly related to gross rents per unit of capital and the slope coefficients are the same for all firms.
Again, there is nothing tautological about this. Timing effects can make the selection term perverse. For example, if the firms that by time T have most adapted their decision rules to accommodate the change in prices do their adapting late in the game relative to firms that only adapt a little, the selection term can have the wrong sign. Or a perverse effect is possible if the m arginal relationship between (quasi-rent) returns to capital and the firm growth rate is different for different firms, and systematically related to interfirm differences in intensity of use of the input whose price has changed. Imagine, for example, that there are two groups of firms, the first with a labor capital ratio that is 10 p ercent lower than the second. Suppose that initial total capital in the two groups is the same, but investment by labor-intensive firms hardly responds to profitability at all, while in the other group half of any “excess return” on capital is reinvested. A fall in the wage rate will encourage investment by both groups. Although the capital-intensive group enj oys a smaller increase in profitability, its investment policies translate this into a larger in crease in growth rate. Thus, abstracting from rule-induced changes and the effects of the wage rate decline on search, considering only selection effects, the average labor-capital ratio in the industry falls with a decline in the wage.
Obviously, our accounting scheme does not do full justice to the richness of the possible behavioral relationships and dynamic in teractions linking routinized response, search, and selection. Formal dynamic models incorporating these mechanisms can be con structed, and explored analytically or with simulation. In the explo ration of a particular dynamic model, our accounting scheme may re tain heuristic value, but the specific assumptions of the model would necessarily take over the center of the stage.
The discussion above has been quite general. We have demon strated that it is plausible to think of “along the rule,” “search,” and “selection” as involving different aspects of firm behavior and that under plausible. models the effects of each of these mechanisms would be standard. Although specific perverse cases can be con structed, it seems unlikely that it would be possible to produce a plausible model in which an overall perverse result would hold in general, independent of particular initial conditions and parameter values. The qualitative predictions of orthodox comparative statics analysis may well describe the typical patterns of firm and i ndustry response in the dynamic, evolving economy of reality. However, evolutionary analysis probes more deeply into the explanations for these patterns and warns of possible exceptions. Also, the explicit recognition of the search and selection components of adjustment brings a whole new range of phenomena into theoretical view.
Source: Nelson Richard R., Winter Sidney G. (1985), An Evolutionary Theory of Economic Change, Belknap Press: An Imprint of Harvard University Press.
