In section 6.2, we have just seen how the principal and the agent can achieve ex post efficiency through an ex ante contract when they are both risk neutral. This contract uses only the agent’s message but fails to achieve efficiency when the agent is risk-averse or when nonresponsiveness occurs. We now propose a slightly more complicated implementation of the ex post efficient allocation that also works in these cases. The new feature of this implementation comes from the fact that both the principal and the agent must now send a report on the state of nature at date t = 2. Requesting both the principal and the agent to report the state of nature moves us somewhat beyond the technics that have been the focus of this volume. This extension is only a small detour into a multiagent setting. It is needed to assess the true importance of the nonverifiability constraint in principal-agent models.
The principal now offers to play a game with the agent, the outcome of which is enforced by the uniformed court of law. In this game, the principal is, like the agent, an active player, so that the mechanism to be played is a two-player game. However, as this game is played ex post under complete information, the characterization of the optimal two-player mechanism is relatively straightforward.
In this context, a general mechanism should involve two message spaces, one for the principal, say Mp, and one for the agent, Ma. Still denoting by d the set of feasible allocations, we have the following definition:
Definition 6.1:A mechanism is a pair of message spaces Ma and Mp and a mapping g(-) from M = Ma x Mp into A, which writes as g˜(ma, mp) = (q˜(ma, mp), t˜(ma, mp)) for all pairs (ma, mp) belonging to M.
To fix ideas, let us assume that the principal and the agent have respective utility functions V = S(q, θ) − t and U = t − C(q, θ). In this context, the first-best allocation rule a∗(θ) = (t∗(θ), q∗(θ)) is such that

We consider that those traders play a Nash equilibrium6 of the mechanism (M, g˜(·)).
A Nash equilibrium of the mechanism (M, g˜(·)) is a pair of message functions (ma∗(·), mp*(·)), which satisfy the following incentive conditions: for the principal,

and for the agent,

According to (6.7), when the principal conjectures that the agent’s strategy is given by ![]() in state θ, his best response is
in state θ, his best response is ![]() . Similarly, (6.8) states that the agent’s strategy
. Similarly, (6.8) states that the agent’s strategy ![]() is a best response to the principal’s behavior.
is a best response to the principal’s behavior.
We can now state the definition that follows:
Definition 6.2: An allocation rule a(θ) from Θ to ” is implementable in Nash equilibrium by a mechanism (M, g˜(·)) if there exists a Nash equilib- rium ![]() for all θ in Θ.
for all θ in Θ.
When the message spaces Ma and Mp are reduced to the set of possible types Θ, we have the following definitions:
Definition 6.3: A direct revelation mechanism is a mapping g(·) from Θ2 to A, which writes as ![]() is the agent’s (resp. principal’s) report in Θ.
is the agent’s (resp. principal’s) report in Θ.
Definition 6.4: A direct revelation mechanism g(·) is truthful if it is a Nash equilibrium for the agent and the principal to report truthfully the state of nature.
Denoting the set of Nash equilibria of the direct revelation mechanism g(·) in state θ by Ng(θ), we have the following definition:
Definition 6.5: The allocation a(θ) is implementable in Nash equilib-rium by the direct revelation mechanism g(·) if the pair of truthful report-ing strategies of the principal and the agent forms a Nash equilibrium of g(·) ((θ, θ) in Ng(θ) for all θ in Θ) such that a(θ) = g(θ, θ) for all θ in Θ.
Truthful direct revelation mechanisms must thus satisfy the following Nash incentive constraints:

and

We can now prove a new version of the revelation principle in this complete information environment.
Proposition 6.1: Any allocation rule a(θ) that is implemented in Nash equilibrium by a mechanism (M, g˜(·)) can also be implemented in Nash equilibrium by a truthful direct revelation mechanism.
Proof: The mechanism (M, g˜(·)) induces an allocation rule ![]()
![]() are the messages of the agent and the principal in state θ at the Nash equilibrium of (M, g˜(·)) that we consider. Let us define a direct revelation mechanism g(·) from Θ2 into A, such that g(θ, θ) =
are the messages of the agent and the principal in state θ at the Nash equilibrium of (M, g˜(·)) that we consider. Let us define a direct revelation mechanism g(·) from Θ2 into A, such that g(θ, θ) = ![]() . For all states of nature θ, we have thus
. For all states of nature θ, we have thus ![]() . We check that it is a Nash equilibrium for the players to report the truth when they face the direct revelation mechanism g(·). For the principal, we have
. We check that it is a Nash equilibrium for the players to report the truth when they face the direct revelation mechanism g(·). For the principal, we have

Taking ![]() for any θ’ in Θ, we obtain
for any θ’ in Θ, we obtain

Finally, we get

Hence, the principal’s best response to a truthful reporting strategy by the agent is also to report truthfully.
Proceeding similarly for the agent, we prove that the agent’s best response is also to report his type truthfully. Hence, truthful reporting is a Nash equilibrium.
The important question at this point is to determine which restrictions are really put on allocations by the incentive compatibility constraints (6.9) and (6.10). In particular, we would like to know under which conditions the first-best allo- cation rule a∗(θ) = (t∗(θ), q∗(θ)) is implementable as a Nash equilibrium of the direct revelation mechanism played by the principal and the agent. It turns out that incentive compatibility in this multiagent framework imposes very few restrictions on the set of implementable allocations.
To see that, let us first consider the simple case where the principal’s utility function does not depend directly on θ, i.e., his utility is given by V = S(q) − t.

Figure 6.4: Nash Implementation of the First-Best with the No-Trade Option as Punishment
The agent also has the standard linear cost function of chapter 2, U = t − θq. We know that the first-best allocation entails producing outputs q∗(θ), such that S‘(q∗(θ)) = θ. Using transfers t∗(θ) = θq∗(θ) allows then the principal to extract all of the agent’s rent.
A truthful direct revelation mechanism g(·) that implements in Nash equilib- rium the first-best allocation rule a∗(θ) = (t∗(θ), q∗(θ)) can be summarized by a
matrix (Figure 6.4), where the lines (resp. columns) represent the agent’s (resp. principal’s) possible reports in Θ = {θ, θ¯}. In each box of the matrix, we have rep-resented the transfer-output pair corresponding to the reports made by the principal and the agent.
For instance, when both the principal and the agent report to the court that θ has realized, the contract (t∗, q∗) is enforced. The principal gets a net surplus S(q∗) − t∗ = S(q∗) − θq∗, and the agent gets t∗ − θq∗ = 0 if the true state of nature is θ. If they disagree, the no-trade option is enforced, with no output being produced and no transfer being made.
The important point to note is that the same game form must be played by the agent and the principal, whatever the true state of nature θ. Indeed, the state of nature being nonverifiable, the transfers and outputs in each box of the matrix cannot be made contingent upon it. The goal of this mechanism is to ensure that there exists a truthful Nash equilibrium in each state θ that implements the first-best allocation a∗(θ) = (t∗(θ), q∗(θ)).
Proposition 6.2: Assume that preferences are given by V = S(q) − t and U = t − θq, then the first-best allocation rule is Nash-implementable.
Proof: Let us check that truthtelling is a Nash equilibrium of the direct revelation mechanism g(·) in each state of nature. Consider first state θ. Given that the agent reports θ, the principal gets S(q∗) − t∗ = S(q∗) − θq∗ by reporting the truth and zero otherwise. By assumption, trade is valuable when θ realizes (S(q∗) − θq∗ > 0), and telling the truth is a best response for the principal. The agent is indifferent between telling the truth or not when the principal reports θ, because t∗ − θq∗ = 0. Hence, he weakly prefers to tell the truth as a best response. Consider now state θ¯. Given that the agent reports θ¯, the principal gets ![]() by reporting the truth and zero otherwise. By assumption, trade is also valuable when θ¯ realizes
by reporting the truth and zero otherwise. By assumption, trade is also valuable when θ¯ realizes ![]() . Telling the truth is a best response for the principal. Similarly, the agent is indifferent between telling the truth or not when the principal reports truthfully, because
. Telling the truth is a best response for the principal. Similarly, the agent is indifferent between telling the truth or not when the principal reports truthfully, because ![]() . He weakly prefers to tell the truth. This ends the proof that truthtelling is a Nash equilibrium of g(·).
. He weakly prefers to tell the truth. This ends the proof that truthtelling is a Nash equilibrium of g(·).
It is important to note that, when θ realizes, the pair of truthful strategies is not the unique Nash equilibrium of the direct mechanism g(·). Indeed, (θ¯, θ¯) is another Nash equilibrium in this state of nature. The agent strictly gains from misreporting if the principal does so, because ![]() . Also, the principal prefers to report θ¯ if the agent does so, because he obtains
. Also, the principal prefers to report θ¯ if the agent does so, because he obtains ![]() .
.
There are two possible attitudes vis-à vis this multiplicity problem. First, one may forget about it and argue that truth-telling should be a focal equilibrium. This attitude rests on a relatively shaky argument in the absence of a definitive theory of equilibrium selection. Moreover, some authors have shown in related models that the nontruthful equilibrium may sometimes Pareto dominate the truthful one from the players’ point of view.7 In this case, the focus on the truthful equilibrium is less attractive. This argument is less compelling in our context since the two equilibria cannot be Pareto-ranked: the agent does better in the nontruthful equilibrium, than in the truthful one, but the principal does worse.
The second possible attitude towards the multiplicity of equilibria is to take it seriously and to look for mechanisms that ensure that the first-best allocation is uniquely implementable. This second attitude is the route we are going to take now.
Definition 6.6: The first-best allocation rule a∗(θ) is uniquely imple- mentable in Nash equilibrium by the mechanism (M, g˜(·)) if the mecha- nism has a unique Nash equilibrium for each θ in Θ and it induces the allocation a∗(θ).
In the definition above, we do not restrict a priori the mechanism g˜(·) to be a direct revelation mechanism. It could well be that the cost of obtaining unique implementation is the expansion of the space of messages that the agent and the principal use to communicate with the court. Such extensions are often used in multiagent (three or more) frameworks. In our principal-agent model, those extensions are not needed, provided that one conveniently defines the out- of-equilibrium-path punishments.
For the time being, let us consider a truthful direct revelation mechanism like that shown in figure 6.5.

Figure 6.5: Nash Implementation of the First-Best with General Punishments
The outcomes ![]() may be different from the no-trade option used above, in order to give more flexibility to the court in designing off-the- equilibrium punishments, ensuring both the truthful revelation and the uniqueness of the equilibrium. Let us now see how it is possible to do so.
may be different from the no-trade option used above, in order to give more flexibility to the court in designing off-the- equilibrium punishments, ensuring both the truthful revelation and the uniqueness of the equilibrium. Let us now see how it is possible to do so.
The conditions for having a truthful Nash equilibrium in state θ are, for the principal,
![]()
and for the agent
![]()
Similarly, the conditions for having a truthful Nash equilibrium in state θ¯ are, for the principal,
![]()
and for the agent,
![]()
Let us now turn to the conditions ensuring that there is no nontruthful, pure- strategy Nash equilibrium in either state of nature. Consider a possible nontruthful equilibrium ![]() when state θ realizes. Given that (6.13) is needed to satisfy the principal’s incentive constraint in state θ¯, the only way to break the possible equilibrium is to induce a deviation by the agent. Therefore, we must have
when state θ realizes. Given that (6.13) is needed to satisfy the principal’s incentive constraint in state θ¯, the only way to break the possible equilibrium is to induce a deviation by the agent. Therefore, we must have
![]()
Now consider a possible nontruthful pure-strategy Nash equilibrium (θ, θ) when state θ¯ realizes. Given that (6.11) is needed to ensure the principal’s incen- tive constraint in state θ, the only way to break the possible equilibrium is again to induce a deviation by the agent:
![]()
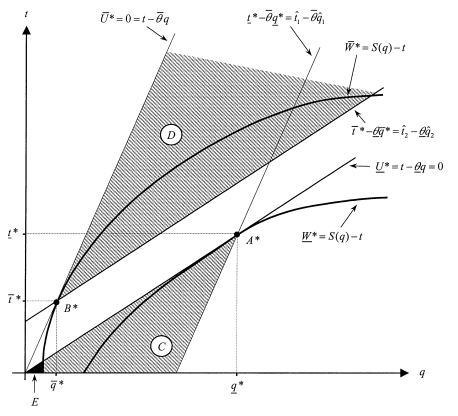
Figure 6.6: Off-the-Equilibrium Path Punishments
A truthful direct revelation mechanism g(·), which uniquely implements the first-best as a Nash equilibrium, exists when the conditions (6.11) through (6.16) are all satisfied by a pair of punishment contracts ![]() . We now have the following proposition:
. We now have the following proposition:
Proposition 6.3: Assume preferences are given by V = S(q) − t and U = t − θq. A truthful direct revelation mechanism g(·) exists that uniquely implements in Nash equilibrium the first-best allocation rule a∗(θ).
Proof: The clearest way of doing this proof is to draw a picture. In Figure 6.6, we have represented the first-best allocation a∗(θ) and the possible punishments ![]() .
.
Because the first-best allocation requires that the agent produce efficiently and gets zero rent, the indifference curves of the principal are tangent to the zero-profit lines of the agent in each state of nature at points A∗ and B∗. First, the θ-agent incentive compatibility constraint (6.12) and the condition (6.16) define a subset C where (tˆ1, qˆ1) may lie (crossed area in figure 6.6). Within this subset, the principal’s incentive constraint (6.13) further reduces the set of possible punishments (tˆ1, qˆ1) to the area E close to the origin (shaded area in figure 6.6). This set is nonempty, because the principal’s indifference curve W¯* = S(q) − t does not go through the origin when trade is valuable in state θ¯ (namely when ![]() ).
).
Similarly, the agent’s incentive constraints (6.14) and (6.15) define a subset D of possible values for the punishment ![]() (crossed area in figure 6.6). In figure 6.6, this full set satisfies the principal’s incentive compatibility constraint (6.11). More generally, by strict concavity of the principal’s indifference curve W¯* = S(q) − t going through B∗, there exists a nonempty subset of D that lies strictly above this indifference curve. All those points obviously lie above the prin- cipal’s indifference curve W ∗ = S(q) − t going through A∗.
(crossed area in figure 6.6). In figure 6.6, this full set satisfies the principal’s incentive compatibility constraint (6.11). More generally, by strict concavity of the principal’s indifference curve W¯* = S(q) − t going through B∗, there exists a nonempty subset of D that lies strictly above this indifference curve. All those points obviously lie above the prin- cipal’s indifference curve W ∗ = S(q) − t going through A∗.
Proposition 6.3 yields a very striking result. It says that direct revelation mech- anisms are enough to ensure efficiency always if the court can design punishments in a clever way. There is no need to use more complex mechanisms in this simple and rather structured principal-agent model.
More generally, one may wonder if the requirement of unique Nash imple- mentation imposes some structure on the set of allocation rules a(θ) = (t(θ), q(θ)) that can be implemented this way. Indeed, this structure exists. Before describing it, we need another definition, which we cast in the general case where the prin- cipal’s and the agent’s preferences are respectively given by V = S(q, θ) − t and U = t − C(q, θ).
Definition 6.7: An allocation rule a(θ) = (t(θ), q(θ)) is monotonic if and only if for any θ in Θ, such that a(θ) # a(θ’) for some θ‘ in Θ, there exists an allocation (tˆ, qˆ) such that one of the two conditions below is true:

These inequalities have a simple meaning.8 The allocation rule a(·) selects the pair a(θ) = (t(θ), q(θ)) in state θ and not in state θ‘, if there exists another allocation (tˆ, qˆ) such that either the principal or the agent prefers this allocation to a(θ) when the state of nature is θ‘.
Under the assumptions of proposition 6.3, the first-best allocation rule a∗(·) is monotonic. Indeed, first we note that a∗(θ) # a∗(θ¯). Second, the principal’s utility function being independent of θ, there does not exist any allocation (tˆ, qˆ) such that condition (P ) holds. Lastly, there exists (tˆ, qˆ) such that condition (A) holds. In state θ, the set of such pairs is the set C in figure 6.6. In state θ¯, it is the set D. The monotonicity of allocation rules is an important property that follows immediately from unique implementation in Nash equilibrium, as is shown in proposition 6.4.
Proposition 6.4: Consider an allocation rule a(·), which is uniquely implemented in Nash equilibrium by a mechanism (M, g˜(·)); then the allocation rule a(·) is monotonic.
Proof: The mechanism (M, g˜(·)) uses the message spaces Ma and Mp. If the allocation rule a(-) is uniquely implementable in Nash equilibrium by g˜(-), we know that, in state 0, there exists a pair of strategies ![]() such that
such that ![]() , and these strategies form a Nash equilibrium
, and these strategies form a Nash equilibrium

Moreover, a(θ) being different from a(θ‘) for a θ‘ different from θ, a(θ) is not a Nash equilibrium in state θ‘. This means that either the principal (or the agent) finds it strictly better to send a message m˜p rather than ![]() (or m˜a rather than
(or m˜a rather than ![]() in the case of the agent). For the principal, this means that
in the case of the agent). For the principal, this means that
![]()
For the agent, this means that
![]()
In each case, it is easy to show that the allocation rule a(·) is monotonic. Take ![]() in the first case (the principal’s devi-ation) and
in the first case (the principal’s devi-ation) and ![]() in the second case (the agent’s deviation).
in the second case (the agent’s deviation).
The intuitive meaning of proposition 6.4 is rather clear. In order to prevent an allocation implemented in one state of nature θ to be also chosen in another state θ‘, either the principal or the agent must deviate and choose another message in state θ‘. Hence, the mechanism g˜(·) that uniquely implements the allocation rule a(·) must include an allocation (tˆ, qˆ), which is worse than (t(θ), q(θ)) for both agents in state θ but better for at least one in state θ‘. In this case, the latter player’s preferences are reversed between states θ and θ‘, breaking a possible equilibrium that would also implement a(θ) in state θ‘.
The monotonicity property is a necessary condition satisfied by an allocation rule that is uniquely implementable in Nash equilibrium.
The remaining question is to know how far away this property is from suf- ficiency. With more than two agents (n ≥ 3), Maskin (1999) shows that monotonicity plus another property, no veto power, is also sufficient for unique Nash implementation. With two agents only, Dutta and Sen (1991) and Moore and Repullo (1990) have provided necessary and sufficient con- ditions for unique Nash implementation in more general environments than the principal-agent relationship analyzed in this chapter.
Source: Laffont Jean-Jacques, Martimort David (2002), The Theory of Incentives: The Principal-Agent Model, Princeton University Press.
