From proposition 6.4, a necessary condition for unique Nash implementation is that an allocation rule a(·) be monotonic. Any allocation rule that fails to be monotonic will also fail to guarantee unique Nash implementation. Then, one may wonder if refinements of the Nash equilibrium concept can still be used to ensure unique implementation. The natural refinement of subgame perfection will appear when one moves to a game with sequential moves, where the principal and the agent take turns sending messages to the court. An allocation rule a(θ) is uniquely implementable in subgame-perfect equilibrium by a mechanism g¯(·) provided that its unique subgame-perfect equilibrium yields allocation a(θ) in any state θ.
Instead of presenting the general theory of subgame-perfect implementation, which is quite complex, we propose a simple example showing the mechanics of the procedure. Let us first single out a principal-agent setting where the first- best allocation rule is nonmonotonic. As we know from the last section, this calls for a more complex modelling of information than what we have used so far if we remain in the context of principal-agent models with quasi-linear objective functions. Consider a principal with utility function V = S(q) − t independent of the state of nature θ. For simplicity, we assume that 
, where µ and λ are common knowledge. The agent instead has a utility function U = 
, where θ = (θ1 ,θ2) is now a bidimensional state of nature.
The first-best outputs q∗(θ1, θ2) are given by the first-order conditions S‘(q∗(θ1, θ2)) = θ1 + θ2q∗(θ1, θ2). We immediately find that 
.
We assume that each parameter θi belongs to 
. A priori, there are four possible states of nature and four first-best outputs. Assuming that 
i.e., µ − λ = θ + θ¯, we are left with three first-best outputs 
1, and 
that we assume to be all positive.
Of course, even if the production level is the same in states 
, the agent has different costs and should receive different transfers 
from the principal in those two states of nature. We denote by t∗ and t¯∗ the transfers in the other states of nature.
In figure 6.7, we have represented the first-best allocations corresponding to the different states of nature.
Importantly, the indifference curve of a (θ, θ¯)-agent going through the first- best allocation C∗ of a (θ, θ¯)-agent (dotted curve in figure 6.7) is tangent to and always above that of a (θ¯, θ)-agent.11 This means that one cannot find any allo- cation (tˆ, qˆ) such that condition (A) of definition 6.6 holds. In other words, the first-best allocation rule a∗(θ) is nonmonotonic in this bidimensional example. To see more precisely why it is so, note that any mechanism g˜(·) implementing the first-best allocation a∗(θ¯, θ) must be such that
Figure 6.7: First-Best Allocations
But, since the indifference curve of a (θ, θ¯)-agent through C∗ is above the one of a (θ¯, θ)-agent, this inequality also implies that
Since the principal’s utility function does not depend directly on θ, the pair of strategies 
that implements the allocation 
remains an equilibrium in state 
. Hence, there is no hope of finding a unique Nash implementation of the first-best outcome.
Let us now turn to a possible unique implementation using a three-stage extensive form mechanism and the more stringent concept of subgame-perfection. The reader should be convinced that there is not too much problem in elicit-ing the preferences of the agent in states (θ, θ) and (θ¯, θ¯). Hence, we will focus on a “reduced” extensive form that is enough to highlight the logic of subgame- perfect implementation. The objective of this extensive form is to have the agent truthfully reveal the state of nature when either (θ¯, θ) or (θ, θ¯) occurs.
Figure 6.8: Subgame-Perfect Implementation
In figure 6.8 we have represented such an extensive form.
The mechanism to be played in both states (θ, θ¯) and (θ¯, θ) is a three-stage game with the agent moving first and announcing whether (θ,θ¯) or (θ¯, θ) has been realized. If (θ, θ¯) is announced, the game ends with the allocation 
. If (θ¯, θ) is announced, the principal may agree and then the game ends with the allocation 
or challenge. In the latter case, the agent has to choose between two possible out-of-equilibrium allocations 
. We have a greater flexibility with respect to Nash implementation, since now the agent has sometimes to choose between two allocations that are nonequilibrium ones instead of between an out-of-equilibrium one and an equilibrium one, as under Nash implementation. We want to use this flexibility to obtain in the state of nature (θ, θ¯) and in the state of nature (θ¯, θ). To do so, we are going to choose the allocations in such a way that the agent prefers a different allocation in different states of the world.Specifically, we choose them to have
and
Then, since at stage 3 the agent chooses 
in state (θ¯, θ), to obtain the principal should not be willing to challenge the agent’s report at stage 2 of the game. This means that one should have
Finally, the agent with type (θ¯, θ) should prefer to report truthfully that (θ¯, θ) has realized, i.e.:
Now let us see how we can obtain in the state of nature (θ, θ¯). Since the agent chooses in state (θ, θ¯), the principal should be willing to chal- lenge, i.e.,
Expecting this behavior by the principal, the agent should not be willing to announce (θ¯, θ) when the state of nature is (θ, θ¯). This means that the following inequality must also hold:
The remaining question is whether there exists a pair of contracts and 
that satisfy constraints (6.21) to (6.26). The response can be given graphically (figure 6.9). By definition, (resp. ) should be above (resp. below) the principal’s indifference curve going through C∗. Note that for q > qˆ*, the indifference curves of an agent with (θ, θ¯) have a greater slope than those of an agent with type (θ¯, θ). This helps to construct very easily the out-of-equilibrium allocations , as in figure 6.9.
Remark: Subgame-perfect implementation is beautiful and attractive, but it should be noted that it has been sometimes criticized because it relies excessively on rationality. The kind of problem at hand can be illustrated with our example of figure 6.8. Indeed, when state (θ, θ¯) realizes and the principal has to decide to move at the second stage, he knows that the agent has already made a suboptimal move. Why should he still believe that the agent will behave optimally at stage 3, as needed by subgame-perfect implementation?
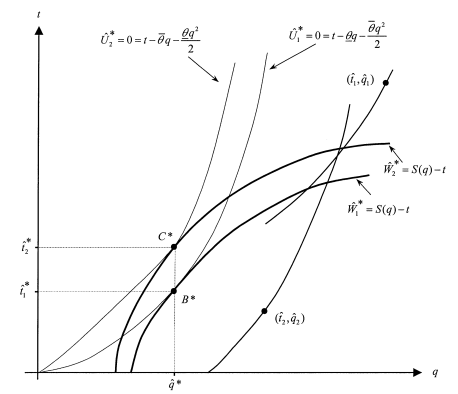
Figure 6.9: Subgame-Perfect Implementation
Moore and Repullo (1988) present a set of conditions ensuring subgame-perfect implementation in general environments, notice-ably those with more than two agents. The construction is rather complex but close in spirit to our example. Abreu and Matsushima (1992) have developed the concept of virtual-implementation of an allocation rule. The idea is that the allocation rule may not be implemented with probability one but instead with very high probability. With this implementation concept, any allocation rule can be virtually implemented as a subgame-perfect equilibrium.
Source: Laffont Jean-Jacques, Martimort David (2002), The Theory of Incentives: The Principal-Agent Model, Princeton University Press.