1. Finality
As we have seen, systems of equations of the type considered may have three different kinds of solution. The system in question may asymptotically attain a stable stationary state with increasing time; it may never attain such state; or there may be periodic oscillations. In case the system approaches a stationary state, its variation can be expressed not only in terms of the actual conditions but also in terms of the distance from the stationary state. If Qi* are the solutions for the stationary state, new variables:
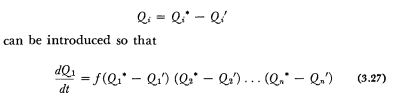
We may express this as follows. In case a system approaches a stationary state, changes occurring may be expressed not only in terms of actual conditions, but also in terms of the distance from the equilibrium state; the system seems to “aim” at an equilibrium to be reached only in the future. Or else, the happenings may be expressed as depending on a future final state.
It has been maintained for a long time that certain formulations in physics have an apparently finalistic character. This applies in two respects. Such teleology was especially seen in the minimum principles Of mechanics. Already Maupertuis considered his minimum principle as proof that the world, where among many virtual movements the one leading to maximum effect with minimum effort is realized, is the “best of all worlds” and work of a purposeful creator. Euler made a similar remark: “Since the construction of the whole world is the most eminent and since it originated from the wisest creator, nothing is found in the world which would not show a maximum or minimum characteristic.” A similar teleological aspect can be seen in Le Chatelier’s principle in physical chemistry and in Lenz’s rule of electricity. All these principles express that in case of disturbance, the system develops forces which counteract the disturbance and restore a state of equilibrium; they are derivations from the principle of minimum effect. Principles homologous to the principle of minimum action in mechanics can be construed for any type of system; thus Volterra (cf. d’Ancona, 1939; pp. 98ff.) has shown that a population dynamics homologous to mechanical dynamics can be developed where a similar principle of minimum action appears.
The conceptual error of an anthropomorphic interpretation is easily seen. The principle of minimum action and related prim ciples simply result from the fact that, if a system reaches a state of equilibrium, the derivatives become zero; this implies that certain variables reach an extremum, minimum or maximum; only when these variables are denoted by anthropomorphic terms like effect, constraint, work, etc., an apparent teleology in physical processes emerges in physical action (cf. Bavink, 1944).
Finality can be spoken of also in the sense of dependence on the future. As can be seen from equation (3.27), happenings can, in fact, be considered and described as being determined not by actual conditions, but also by the final state to be reached. Secondly, this formulation is of a general nature; it does not only apply to mechanics, but to any kind of system. Thirdly, the question was frequently misinterpreted in biology and philosophy, so that clarification is fairly important.
Let us take, for a change, a growth equation formulated by the author (von Bertalanffy, 1934 and elsewhere). The equation is: l = l* — (l* — l0e-kt) (cf. pp. 17Iff.), where l represents the length of the animal at time t, l* the final length, l0 the initial length, and k a constant. This looks as if the length l of the animal at time t were determined by the final value l* which will be reached only after infinitely long time. However, the final state (/*) simply is an extremum condition obtained by equating the differential quotient to zero so that t disappears. In order to do so, we must first know the differential equation by which the process is actually determined. This differential equation is:
and states that growth is determined by a counteraction of processes of anabolism and catabolism, with parameters E and k respectively. In this equation, the process at time t is determined only by the actual conditions and no future state appears. By equating to zero, l* is defined by E/k. The “teleological” final-value formula therefore is only a transformation of the differential equation indicating actual conditions. In other words, the directedness of the process towards a final state is not a process differing from causality, but another expression of it. The final state to be reached in future is not a “vis a fronte” mysteriously attracting the system, but only another expression for causal “vires a tergo.” For this reason, physics makes ample use of such final-value formulas because the fact is mathematically clear and nobody attributes an anthropomorphic “foresight” of the goal to a physical system. Biologists, on the other hand, often regarded such formulas as somewhat uncanny, either fearing a hidden vitalism, or else considering such teleology or goal-directedness as “proof” for vitalism. For with respect to animate rather than to inanimate nature, we tend to compare finalistic processes with human foresight of the goal; while, in fact, we are dealing with obvious, even mathematically trivial relations.
This matter was frequently misinterpreted even by philosophers. From E. von Hartmann to modern authors like Kafka (1922) and myself, finality was defined as the reverse of causality, as dependence of the process on future instead of past conditions. This was frequently objected to because, according to this conception, a state A would depend on a state B in the future, an existent on a non-existent (e.g., Gross 1930; similarly Schlick). As the above shows, this formulation does not mean an inconceivable “action” of a not existent future, but merely a sometimes useful formulation of a fact which can be expressed in terms of causality.
2. Types of Finality
No detailed discussion of the problem of finality is intended here, but enumeration of several types may be useful. Thus we can distinguish:
(1) Static teleology or fitness, meaning that an arrangement seems to be useful for a certain “purpose.” Thus a fur coat is fit to keep the body warm, and so are hairs, feathers, or layers of fat in animals. Thorns may protect plants against grazing cattle, or imitative colorations and mimicries
may be advantageous to protect animals against enemies.
(2) Dynamic teleology, meaning a directiveness of processes. Here different phenomena can be distinguished which are often confused:
(i) Direction of events towards a final state which can be expressed as if the present behavior were dependent on that final state. Every system which attains a timeindependent condition behaves in this way.
(ii) Directiveness based upon structure, meaning that an arrangement of structures leads the process in such way that a certain result is achieved. This is true, of course, of the function of man-made machines yielding products or performances as desired. In living nature we find a structural order of processes that in its complication widely surpasses all man-made machines. Such order is found from the function of macroscopic organs, such as the eye as a sort of camera or the heart as a pump, to microscopic cell structures responsible for metabolism, secretion, excitability, heredity and so forth. Whilst man-made machines work in such a way as to yield certain products and performances, for example, fabrication of airplanes or moving a railway train, the order of process in living systems is such as to maintain the system itself. An important part of these processes is represented by homeostasis (Canon)—i.e., those processes through which the material and energetical situation of the organism is maintained constant. Examples are the mechanisms of thermoregulation, of maintenance of osmotic pressure, of pH, of salt concentration, the regulation of posture and so forth. These regulations are governed, in a wide extent, by feedback mechanisms. Feedback means that from the output of a machine a certain amount is monitored back, as “information,” to the input so as to regulate the latter and thus to stabilize or direct the action of the machine. Mechanisms of this kind are well known in technology, as, for instance, the governor of the steam-engine, self-steering missiles and other “servomechanisms.” Feedback mechanisms appear to be responsible for a large part of organic regulations and phenomena of homeostasis, as recently emphasized by Cybernetics (Frank et al., 1948; Wiener, 1948).
(iii) There is, however, yet another basis for organic regulations. This is equifinality—i.e., the fact that the same final state can be reached from different initial conditions and in different ways. This is found to be the case in open systems, insofar as they attain a steady state. It appears that equifinality is responsible for the primary regulability of organic systems—i.e., for all those regulations which cannot be based upon predetermined structures or mechanisms, but on the contrary, exclude such mechanisms and were regarded therefore as arguments for vitalism.
(iv) Finally, there is true finality or purposiveness, meaning that the actual behavior is determined by the foresight of the goal. This is the original Aristotelian concept. It presupposes that the future goal is already present in thought, and directs the present action. True purposiveness is characteristic of human behavior, and it is connected with the evolution of the symbolism of language and concepts (von Bertalanffy, 1948a, 1965).
The confusion of these different types of finality is one of the factors responsible for the confusion occurring in epistemology and theoretical biology. In the field of man-made things, fitness (a) and teleological working of machines (b, ii) are, of course, due to a planning intelligence (b, iv). Fitness in organic structures (a) can presumably be explained by the causal play of random mutations and natural selection. This explanation is, however, much less plausible for the origin of the very complicated organic mechanisms and feedback systems (b, ii). Vitalism is essentially the attempt to explain organic directiveness (b, ii and iii) by means of intelligence in foresight of the goal (b, iv). This leads, methodologically, beyond the limits of natural science, and is empirically unjustified, since we have, even in the most astonishing phenomena of regulation or instinct, no justification for, but most definite reasons against, the assumption that for example an embryo or an insect is endowed with superhuman intelligence. An important part of those phenomena which have been advanced as “proofs of vitalism,” such as equifinality and anamorphosis, are consequences of the char-acteristic state of the organism as an open system, and thus accessible to scientific interpretation and theory.
Source: Bertalanffy Ludwig Von (1969), General System Theory: Foundations, Development, Applications, George Braziller Inc.; Revised edition.