1. A Discrete Model
Let us extend the model of chapter 4 by allowing more than two levels of effort. Consider the more general case, with n levels of production q1 < q2 < … < qn and K levels of effort with 0 = e0 < e1 < … < eK—1 and the disutilities of effort ψ(ek) = ψk for all k in {0,… , K — 1}. We still make the normalization ψ0 = 0 and assume that ψk is increasing in k. Let πik for i in {1, … , n} also denote the probability of producing qi when the effort level is ek. Let Si = S(qi) denote the value for the principal of production qi for i in {1, … , n}. The agent still has a separable utility function over monetary transfer and effort U = u(t) — ψ(e), where u(-) is increasing and concave (u’ > 0 and u” < 0) with the normalization u(0) = 0. In such an environment, a contract is a set of transfers {(t1, … tn)} corresponding to all possible output levels. As in chapter 4, we proceed in two steps. First, we compute the second-best cost of inducing effort ek for the principal. We denote this cost by Cp. Second, we find the optimal level of effort from the principal’s point of view, taking into account both the costs and benefits of each action ek.
Let us thus denote by (Pk) the cost minimization problem of a principal willing to implement effort ek. Using our by now standard change of variables, the important variables are the utility levels in each state of nature, i.e., ui = u(ti) or alternatively ti = h(ui) where h = u−1 is increasing and convex (h‘ > 0 and h” > 0). (Pk) is now a convex problem that is written as:

(5.1) is the incentive constraint preventing the agent from exerting effort ek , for k‘ = k when the principal wants to implement effort ek. There are K − 1 such constraints. (5.2) is the agent’s participation constraint when he exerts effort ek. We denote the multiplier of (5.1) by λkk’ and still, as in chapter 4, the multiplier of (5.2.) by μ. The value of this problem is the second-best cost of implementation CkSB for effort ek.
It should be immediately clear that the second-best cost of implementing effort ek is such that CkSB ≥ CkFB = h(ψk), where CkFB denotes the first-best cost of implementing effort ek. This is so because the presence of incentive constraints in problem (Pk) implies that the value of this problem is necessarily not less than under complete information. Note that the inequality above is strict whenever one of the incentive constraints in (5.1) is binding at the optimum of (Pk).
The necessary and sufficient first-order conditions for the optimization of pro- gram (Pk) are thus written as
![]()
where tik is the transfer given to the agent in state i when the principal wants to implement effort ek.
The new difficulty coming from more than two levels of effort is that there may be several incentive constraints binding, i.e., several multipliers λkk’ that may be different from zero. Looking only at local incentive constraints may not be enough to characterize the solution to (Pk), and the optimal payments are then the solutions of a complex system of nonlinear equations. However, if the only binding incentive constraint is the local downward incentive constraint, the first- order condition for problem (Pk) is written simply as
![]()
When the cumulative distribution function of production is a convex function of the level of effort, and when MLRP holds, the local approach described above can be validated, as has been shown by Grossman and Hart (1983). We prove this proposition in section 5.1.3 for the case of a continuum of effort levels and a continuum of performances, but the same kind of proof also applies in this discrete framework.
Even if describing the behavior of the second-best cost of implementation CkSB is in general a difficult task, one may try to get some insights on how the principal chooses the second-best level of effort. The optimal second-best effort is indeed defined as ![]() .
.
Finding this second-best effort eSB is a rather difficult problem and there is, a priori, no reason to be sure that it is below its first-best value. Under- as well as over-provision of effort may now be obtained at the second-best effort.
Under-provision was obtained in chapter 4. To understand how over-provision may also arise, let us consider the following example with three possible levels of effort e0, e1, and e2, and two possible outcomes yielding S‾ and S to the principal. The probabilities that S¯ is realized are, respectively, π0, π1 and π2, with π0 < π1 < π2 and the corresponding disutilities of effort being ψ0 = 0 < ψ1 < ψ2. Under complete information, the intermediate effort is chosen when
![]()
The first inequality means that effort e1 is preferred to e0. The second inequal- ity means that e1 is also preferred to e2.
Under moral hazard, let us first observe that the first-best effort e1 may no longer be implementable. Indeed, let us denote by u¯ and u the levels of utility offered to the agent when S¯ and S realize. Incentive compatibility requires that
![]()
so that the agent prefers exerting effort e1 rather than e0. Similarly, we must also have

to ensure that the agent prefers exerting effort e1 than e2. However, when ![]()
![]() the set of payoffs (u‾, u), such that (5.6) and (5.7) are both satisfied, is empty. Hence, e1 can no longer be implemented.
the set of payoffs (u‾, u), such that (5.6) and (5.7) are both satisfied, is empty. Hence, e1 can no longer be implemented.
Effort e0 remains obviously implementable with a null payment in each state of nature. Finally, effort e2 is implemented when the incentive constraint
![]()
which ensures that effort e2 is preferred to both e1 and e0, and the participation constraint
![]()
are both satisfied.
When ![]() , the maximand on the right-hand side of (5.8) is
, the maximand on the right-hand side of (5.8) is ![]() .
.
Hence, the second-best cost of implementing effort e2 can easily be computed as
![]()
Therefore, effort e2 is second-best optimal when
![]()
It is easy to check that one can find values of S¯− S, so that (5.5) and (5.11) both hold simultaneously. Our conclusion is in proposition 5.1.
Proposition 5.1: With more than two levels of effort, the second-best effort level may be greater than the first-best level.
2. Two Outcomes with a Continuum of Effort Levels
To reduce the cumbersome difficulty of the discrete case, modellers have often preferred to allow for a continuum of effort levels. With more than two states of nature, one meets the soon-important technical problems analyzed in section 5.1.3. With only two possible levels of performance, the analysis nevertheless remains very tractable as we will demonstrate in this section. To make some progress in this direction, we reparameterize the model by assuming that π(e) = e, for all e in [0, 1]. Hence, the agent’s effort level equals the probability of a high perfor- mance. The disutility of effort function efeg is increasing and convex in e (ψ’ > 0 and ψ” > 0) with ψ(0) = 0. Moreover, to ensure interior solutions, we assume that the Inada conditions ψ'(0) = 0 and ψ'(1) = +œ both hold. Let us finally consider a risk-neutral agent with zero initial wealth who is protected by the limited liability constraints

Faced with an incentive contract ![]() , this agent chooses an effort e, such that
, this agent chooses an effort e, such that
![]()
By strict concavity of the agent’s objective function, the incentive constraint rewrites with the following necessary and sufficient first-order condition:
![]()
The principal’s program becomes

As in the model of section 4.3, the limited liability constraint in (5.12) (resp.(5.13)) is again binding (resp. slack). Replacing t¯ with ψ'(e) in the principal’s objective function, the principal’s reduced program (P’) is written as
![]()
When ψ”’ > 0 the principal’s objective function is strictly concave in e, and direct optimization leads to the following equation defining the second-best level of effort eSB:
![]()
This second-best effort is obviously lower than the first-best effort e∗, which is defined by
![]()
The first-best effort is such that the marginal benefit ΔS of increasing effort by a small amount de is just equal to the marginal disutility of doing so ψ’(e∗)de.
Under moral hazard, the marginal benefit ΔSde must be equal to the marginal cost ψ'(eSB)de plus the marginal cost of the agent’s limited liability rent eSBψ”(eSB)de.
Indeed, with moral hazard the limited liability rent of the agent is strictly positive because this rent is also rewritten as EUSB = eSBψ'(eSB) — ψ(eSB) > 0, where the right-hand side inequality is derived from the convexity of ψ(), ψ(0) = 0, and the fact that eSB > 0. Reducing this rent, which is costly from the principal’s point view, calls for decreasing effort below the first-best.
Remark: The model with a risk-neutral agent protected by limited lia- bility bears some strong resemblance to the adverse selection model of chapter 2. Indeed, in both models the principal reduces the expected volume of trade with the agent to reduce the latter’s information rent. Distortions in effort are now replacing distortions in output to reduce this information rent.
3. The First-Order Approach
Let us now consider the case where the risk-averse agent may exert a continuous level of effort e in a compact interval [0, e¯] and by doing so incurs a disutility efeg which is increasing and convex (ψ’ > 0 and ψ” > 0) with ψ(0) = 0. To avoid corner solutions, we will also assume that the Inada conditions ψ(0) = 0 and ψ'(e¯) = +∞ are satisfied.
The agent’s performance q˜ may take any possible value in the compact inter- val Q = [q, q¯] with the conditional distribution F(q|e) and the everywhere positive density function f(q|e). We assume that F(·|e) is twice differentiable with respect to e and that those distributions all have the same full support Q.
Formally, a contract htfq˜gk that implements a given level of effort e must now satisfy the following incentive constraints:

and the participation constraint
![]()
The principal’s problem is thus

We denote by {(tSB(·), eSB)} the solution to (P). The first difficulty with this problem is to ensure that such an optimum exists within the class of all admissible functions t(·). For instance, Mirrlees (1999) has shown that the problem may sometimes have no optimal solution in the class of unbounded sharing rules. The difficulty here comes from the lack of compacity of the set of incentive feasible contracts.6 We leave aside these technicalities to focus on what we think is the main difficulty of problem (P)—simplifying the infinite number of global incentive constraints in (5.18) and replacing those constraints by the simpler local incentive constraint:
![]()
which is a necessary condition if the optimal effort level is positive.
This constraint simply means that the agent is indifferent about his choice between effort e and increasing (or decreasing) his effort by an amount de when he receives the compensation schedule {t(q˜)}.
Let us thus define (PR) as the relaxed problem of the principal, where the infinite number of constraints (5.18) have now been replaced by (5.20):

We denote by {(tR(·), eR)} the solution to this relaxed problem. We will first characterize this solution. Then we will find sufficient conditions under which the solution of the relaxed problem (PR) satisfies the constraints of the original problem (P). Hence, we will have obtained a characterization of the solution for problem (P).
Let us first characterize the solution to the relaxed problem (PR). Denoting the multiplier of (5.20) by λ and the multiplier of (5.19) by μ, we can write the Lagrangian L of this problem as
![]()
Pointwise optimization with respect to t(q) yields

The left-hand side of (5.22) is increasing with respect to tR(q), because u” < 0. Provided that λ > 0, MLRP (here in its strict version for simplicity),

guarantees that the right-hand side of (5.22) is also increasing in q. Hence, under MLRP, tR(q) is strictly increasing with respect to q.
Remark: Note that the probability that the realized output is greater than a given q when effort e is exerted is 1 − F(q|e). Let us check that increasing e raises this probability when MLRP holds. We have

where ![]() is the derivative of the log-likelihood of f(·). But, by MLRP, a(q, e) is increasing in q. a(q, e) cannot be everywhere negative, because by definition
is the derivative of the log-likelihood of f(·). But, by MLRP, a(q, e) is increasing in q. a(q, e) cannot be everywhere negative, because by definition ![]()
![]() . Hence, there exists q∗ such that: α(q, e) ≤ 0 if and only if q ≤ q∗. Fe(q|e) is decreasing in q(resp. increasing) on tqi q∗u (resp. [q∗, q¯]. Since F1(q|e) = Fe(q¯|e) = 0, we necessarily have Fe(q|e) ≤ 0 for any q in [q, q¯]. Hence, when the agent exerts an effort e which is greater than e‘, the distribution of output with e dominates the distribution of output with e’ in the sense of first-order stochastic dominance.
. Hence, there exists q∗ such that: α(q, e) ≤ 0 if and only if q ≤ q∗. Fe(q|e) is decreasing in q(resp. increasing) on tqi q∗u (resp. [q∗, q¯]. Since F1(q|e) = Fe(q¯|e) = 0, we necessarily have Fe(q|e) ≤ 0 for any q in [q, q¯]. Hence, when the agent exerts an effort e which is greater than e‘, the distribution of output with e dominates the distribution of output with e’ in the sense of first-order stochastic dominance.
We now show that indeed λ > 0. Let us first denote by eR the effort level solution of (PR). Multiplying (5.22) by f(q|eR) and integrating over [q, q¯] yields

since ![]() . The expectation operator with respect to the distribution of output induced by effort eR is denoted by
. The expectation operator with respect to the distribution of output induced by effort eR is denoted by ![]() . Because u’ > 0, we have μ > 0 and the participation constraint in (5.19) is binding.
. Because u’ > 0, we have μ > 0 and the participation constraint in (5.19) is binding.
Using (5.22) again, we also find

Multiplying both sides of (5.25) by u(tR(q))f(q|eR) and integrating over [q, q¯] yields

where cov(.) is the covariance operator.
Using the slackness condition associated with (5.20), namely ![]()
![]() , we finally get
, we finally get
![]()
Since u(·) and u‘(·) covary in opposite directions, we necessarily have λ ≥ 0. Moreover, the only case where this covariance is exactly zero is when tR(q) is a constant for all q. But then the incentive constraint (5.20) can no longer be satisfied at a positive level of effort. Having proved that λ> 0, we derive the following proposition from above.
Proposition 5.2: Under MLRP, the solution tR(q) to the relaxed problem (PR) is increasing in q.
We can rewrite the agent’s expected utility when he receives the scheme {tR(q)} and exerts an effort e as

where the second line is obtained simply by integrating by parts, and the third line uses the fact that F(q|e) = 0 and F(q¯|e) = 1 for all e.
Since ψ” > 0, u‘ > 0 and tR(q) is increasing when MLRP holds, U(e) is concave in e as soon as Fee(q|e) > 0 for all (q, e). This last property is called the convexity of the distribution function condition (CDFC).
Remark 1: Joined to MLRP, CDFC captures the idea that increasing the agent’s effort also increases, at a decreasing rate, the probability 1 − F(q|e) that the realized output is greater than q.
Remark 2: Note that CDFC may not always hold. Let us assume, for instance, that production is linked to effort as follows: q = e + ∈ where ∈ is distributed on ]−∞, +∞[ with a cumulative distribution function G(·). Then, CDFC implies that the distribution of ∈ has an increasing density, a rather stringent assumption.
Remark 3: It may seem surprising that such stringent assumptions are needed to prove the simple and intuitive result that the agent’s reward increases as his performance increases. However, remember that the dependence of tR(·) on q(which is bad from the insurance point of view) is interesting only to the extent that it creates incentives for effort. For a higher q to be a signal of a high effort, it must be that an increase of effort increases production unambiguously, but also that the informativeness of q about e increases with q (this is ensured by MLRP).
Since U(e) is concave for a solution of the relaxed problem, the first-order condition (5.20) is sufficient to characterize the incentive constraints. Accordingly, the first-order conditions of problem (P ) are the same as those of problem (PR). Proposition 5.3 provides a summary.
Proposition 5.3: Assume that both MLRP and CDFC both hold. If the optimal effort level is positive, it is characterized by the solution of a relaxed problem (PR) using the first-order approach in (5.20). We have {(tSB(·), eSB)} = {(tR(·), eR)}.
This solution {tSB(·), eSB} is then characterized by the binding participation constraint (5.19), the incentive constraint (5.20), and the two first-order conditions of the principal’s problem, namely (5.22) and

Given the highly restrictive assumptions imposed to prove proposition 5.3, the validity of the first-order approach is somewhat limited. Furthermore, when the first-order approach is not valid, using it can be very misleading. The true solution may not even be one among the multiple solutions of the first-order conditions for the relaxed problem.8 As a consequence, most of the applied moral hazard literature adopts the discrete {0, 1} formalization outlined in chapter 4.
An example: Take S(q) = q and the probability distribution of production ![]()
Note that ![]() . This distribution satisfies the MLRP property, since
. This distribution satisfies the MLRP property, since ![]()
Moreover, we have F(q|e)= 1−exp(−q/e). Hence, ![]() 0, i.e., an increase of effort increases production in the first-order stochastic dominance sense. Finally,
0, i.e., an increase of effort increases production in the first-order stochastic dominance sense. Finally, ![]() so that CDFC is not satisfied.
so that CDFC is not satisfied.
The agent has utility function U = 2√t − e2. (5.22) is immediately writ-ten as
![]()
For a high enough status quo utility level U0 of the agent, one can solve the binding participation constraint of the agent, the first order condition (5.20) of the agent’s problem with respect to e, and the first order condition (5.29) of the principal’s problem with respect to e, and obtain the optimal values of the parameters λSB, μSB, and eSB of the transfer function, which becomes
![]()
Note that the agent’s objective function is strictly concave despite the fact that CDFC is not satisfied. Indeed,
![]()
Designing by tFB the sure transfer associated with the first-best, figure 5.1 summarizes the analysis.
With respect to the first-best, the agent is punished for q ≤ q∗ and rewarded for q > q∗. The agent bears some risk that induces him to exert some effort eSB, which depends on U .
The first-order approach has been one of the most debated issues in contract theory in the late seventies and early eighties. Mirrlees (1975) was the first to point out the limits of this approach and argued that it is valid only when the agent’s problem has a unique maximizer.10i11 Later he offered a proof for the use of this approach when the conditions MLRP and CDFC both hold. This proof was corrected by Rogerson (1985a). Finally, Jewitt (1988) offered a direct proof that the multiplier of the local incentive constraint was positive.12 Jewitt also showed that CDFC can be relaxed, pro- vided that the agent’s utility function satisfies further fine properties. Brown, Chiang, Ghosh, and Wolfstetter (1986) provided a condition validating the first-order approach independently of restrictions on the information struc- tures. Aloi (1997) extended the first-order approach to nonseparable utility functions for the agent. Sinclair-Desgagné (1994) generalized the first-order approach to the case where the principal observes several dimensions of the agent’s performance. Grossman and Hart (1983) gave an exhaustive char- acterization of the agent’s incentive scheme. Their approach is based on a complete description of the incentive and participation constraints when the performances take n ≥ 2 values and the agent’s effort belongs to a finite set. Araujo and Moreira (2001) showed how to solve the moral hazard problem in the absence of a first-order approach.
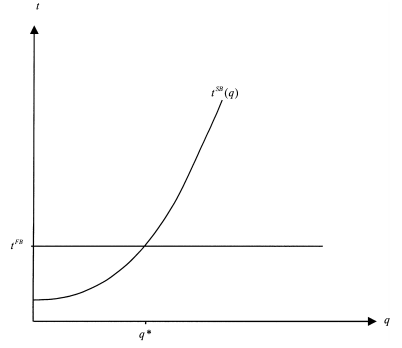
Figure 5.1: First-Best and Second-Best Transfers
Source: Laffont Jean-Jacques, Martimort David (2002), The Theory of Incentives: The Principal-Agent Model, Princeton University Press.
