The previous sections have discussed how various sorts of mechanisms may help to implement the first-best allocation rule when both the principal and the agent are risk neutral. The objective of this section is to discuss the potential of those mechanisms when either the principal or the agent is risk averse.
1. Risk-Averse Agent
When the agent is risk averse, signing no contract ex ante remains optimal if all the bargaining power is still left to the principal ex post. Indeed, ex post take-it-or- leave-it offers impose no risk on the agent, who is always maintained at the zero utility level.
An incentive contract performs badly, because there is now a trade-off between insurance and incentive compatibility. However, the Nash (and subgame-perfect) implementation performs rather well. It is straightforward to extend sections 6.3 and 6.4 to the case of a risk-averse agent to show that Nash implementation allows one to implement the first-best outcome with full insurance for the agent.
2. Risk-Averse Principal
Clearly, signing no contract at the ex ante stage can no longer be optimal even if the principal has all of the bargaining power ex post. Indeed, ex post take-it-or- leave-it offers impose some risk on the principal from an ex ante point of view. However, an incentive contract ![]() can still implement the first-best, as we have seen in section 2.11.2. Making the agent residual claimant for the hierarchy’s profit is again optimal in the case of nonverifiability. Of course, we still have to be sure that nonresponsiveness does not occur.
can still implement the first-best, as we have seen in section 2.11.2. Making the agent residual claimant for the hierarchy’s profit is again optimal in the case of nonverifiability. Of course, we still have to be sure that nonresponsiveness does not occur.
Finally, unique Nash implementation of the first-best outcome can also be obtained using a game form similar to that in figure 6.5. In our standard example, efficiency still requires that q∗ and q¯* are produced, such that S‘(q∗) = θ and ![]() . Providing insurance to the principal also requests that the principal gets the same payoff in each state of nature:
. Providing insurance to the principal also requests that the principal gets the same payoff in each state of nature:
![]()
Finally, the agent’s ex ante participation constraint should also be binding:
![]()
Since trade is more valuable in state θ than in state θ¯, we have ![]()
![]() . Solving (6.27) and (6.28) therefore yields
. Solving (6.27) and (6.28) therefore yields ![]()
![]() .
.
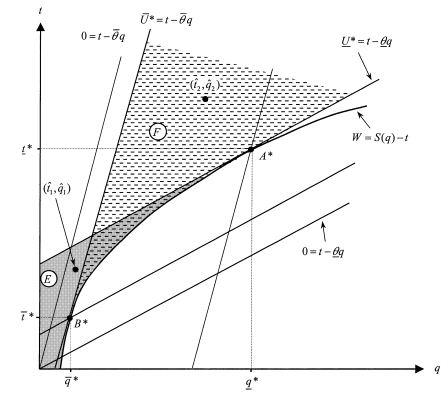
Figure 6.10: Unique Nash Implementation with Risk Aversion
In figure 6.10, we have represented the out of equilibrium contracts ![]() and
and ![]() , which uniquely implement the first-best allocation rule. Proceeding as in Section 6.3, these contracts must again satisfy the following constraints:
, which uniquely implement the first-best allocation rule. Proceeding as in Section 6.3, these contracts must again satisfy the following constraints:

and

We let the reader check that the set E (crossed area) (resp. F (dotted area)) of possible values of ![]() (resp.
(resp.![]() ) satisfying the constraints (6.29) to (6.31) (resp. (6.32) to (6.34)) can be represented as in figure 6.10. In particular, since the areas E and F now have a nonempty intersection,
) satisfying the constraints (6.29) to (6.31) (resp. (6.32) to (6.34)) can be represented as in figure 6.10. In particular, since the areas E and F now have a nonempty intersection, ![]() can be chosen equal to
can be chosen equal to ![]() . Risk aversion on the principal’s side tends to simplify the mechanisms that can be used to implement the first-best.
. Risk aversion on the principal’s side tends to simplify the mechanisms that can be used to implement the first-best.
The above construction may appear somewhat pointless, because simple incentive contracts {t(q)} also achieve the first-best. However, it can be easily extended to common value environments where S(·) is also a function of θ, S(q, θ), and when incentive contracts may run into the difficulties of nonresponsiveness (see sections 2.10.2 and 2.11.1).
Source: Laffont Jean-Jacques, Martimort David (2002), The Theory of Incentives: The Principal-Agent Model, Princeton University Press.
